Which Gimbal scenario is more likely — 30 NM or 10 NM?

[Edward Current]

One result from my Gimbal simulation with clouds is that the object could have taken a straight and level trajectory at around 30 nautical miles. Another result is that it could have taken an increasingly upward, hook-shaped trajectory at 10 NM. Since I uploaded my video on the simulation, people have been arguing for one or the other on Twitter and in my DMs.

Some people are attracted to the 30 NM trajectory because it's minimally simple, like a jet would be flying. Others are attracted to the 10 NM scenario because it's closer to Lt. Ryan Graves' observation of (what he claims was) the Gimbal object coming to a stop and changing direction, inside of 10 NM, as seen on the situational awareness screen.

Meanwhile. . . .
Some people don't like the 30 NM scenario because either Graves would have to be mis-remembering the incident or lying, or the equipment would have to be malfunctioning, or misinterpreted by trained experts, for the object on the SA screen (with its attending "fleet") to be a more distant plane— and, that plane also was not identified as such at the time. On the other hand, some people don't like the 10 NM scenario because it's more like a 3rd-order math function than a physical trajectory of a real-world object.

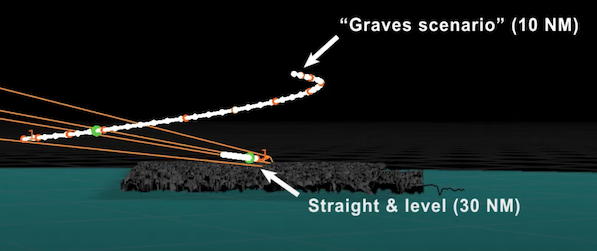
The 10 NM crowd tends to list a number of conditions that needed to be met, and then appeal to incredulity regarding the coincidence required (technical mistake of some kind, camera pointing toward tailpipes, glare artifacts, plane flying in a military training area, transponder off). But coincidences happen, and there's nothing extraordinary about any one of the conditions for the 30 NM scenario. The incident has been selected out of many because it's unusual and unidentified; the ones where a pilot says "Hey, there's Bob" don't get leaked and don't get on 60 Minutes.

The Gish gallop of "impossible coincidences" is a common tactic of bunkers. But typically, they're bringing Occam's razor to a gunfight: If there is even one much bigger necessary condition, then a laundry list of mundane conditions — selected as having coincided from among a large sample size of events — isn't more convincing. Despite the ubiquitous hype.

In my video, I say, "It seems unlikely that such a bizarre trajectory would flatten out to being straight and level farther away." There's a question of how unlikely that is. Given this same F-18 flight path, would all object trajectories derived from various cloud-motion patterns have a straight and level solution somewhere along the sightline? What if the flight path were different? What if the ATFLIR camera elevations were constantly changing, like in GoFast? GoFast seemed to have all straight and level solutions! However, I suspect that if I went back and gave GoFast the same precision treatment that I gave Gimbal, I would find that not to be the case, and that solutions near the water need to bank and/or change altitude to stay in the picture as they did.

I claim that in Gimbal, the hook-shaped 10 NM path is un-physical. Here's why: In a gravity-free vacuum, a vehicle with initial velocity and a thruster of some kind pointing forward–downward, supplying a force that steadily increased in the quantitative sense, might take a jerking path like that. On Earth, with gravity and drag and wind, some other trajectory manifests, even from an ideally increasing thruster...unless we appeal to (1) anti-gravity and anti-drag/wind technology, or (2) technology that compensates for gravity/drag/wind to recover the trajectory that would occur in a gravity-free vacuum. If people are willing to make such appeals, because of their trust in both Graves' and the avionics suite's infallibility— then I say go for it.

Graves remembers the Gimbal object as suddenly coming to a stop and waiting for the "fleet" to pass:

"The wedge formation was flying, let's call it north, then they turned their return radius right into the other direction, which is how aircraft turn. We have to bite into the air. So they turn in the other direction and keep going. Meanwhile, the 'Gimbal' object that was following behind them suddenly stopped and waited for the wedge formation to pass. Then it tilted up like you can see in the clip, and that's when my video cut out, but it just kept following the other five or six, doing like a racetrack pattern."

https://thedebrief.org/devices-of-unknown-origin-part-ii-interlopers-over-the-atlantic-ryan-graves/

If that's an accurate description, it couldn't be referring to the object onscreen. The object suddenly coming to a stop, or even suddenly beginning to slow down, should be reflected in the cloud motion. All of the solutions of the Blender simulation appear to have smooth acceleration or jerk in some direction, from the first frame to the last, with the exception of the one solution where accelerations collapse to zero. Regardless, I'm quite certain that any trajectory coming to a sudden stop (or exhibiting any other sudden change) would not share subspace with a straight and level solution. Smooth, constantly changing trajectories, perhaps...ones with sudden changes — or really, any measurable mid-course change in velocity or its derivatives — no.

Plus:
Even in the case of a randomly generated, smoothly accelerating/jerking trajectory along some camera sightline derived from an arbitrary cloud motion, the corresponding straight and level solution (if any) might be hundreds of miles away. It might be behind the observer. It might require extraordinary speed. But 30 NM is only 3x the distance of 10 NM, and the required speed for a plane at that location (380 knots) happens to be the speed of a plane.

The reason why the 10 NM trajectory is smooth and mathy is that it's a projection of a straight line up the sightline, not a real trajectory in space. I've used this analogy before, but long ago, it was assumed that when a planet in the sky appears to turn around and go retrograde, that's the object's actual path. In reality the object is moving along an ellipse, and the U-ey path is what happens when you view that ellipse from Earth. A random U-ey in the sky does not project to an ellipse in space, unless by sheer coincidence. But the planetary U-eys do. (I'm pretty sure that's why Kepler's ellipse model was so compelling.)

In summary: Realistic, physical trajectories don't work out to straight lines elsewhere on a sightline. Straight lines however do work out to unrealistic, un-physical trajectories elsewhere on the sightline, which is what we have at 10 NM. Or: It's not just that the 30 NM trajectory is minimal. It's that the 10 NM trajectory is a geometrical projection of a minimal trajectory — and, a rather extreme, un-physical one at that.

 

[Mick West]

In summary: Realistic, physical trajectories don't work out to straight lines elsewhere on a sightline. Straight lines however do work out to unrealistic, un-physical trajectories elsewhere on the sightline, which is what we have at 10 NM. Or: It's not just that the 30 NM trajectory is minimal. It's that the 10 NM trajectory is a geometrical projection of a minimal trajectory — and, a rather extreme, un-physical one at that.

I agree. Similarly with the rotating glare observables, for it to be a weird 10NM trajectory, it would almost have to be a craft that is pretending to move in a normal manner, but only from the moving viewpoint of that one jet. This seems like an incredibly more complex assertion (or astounding coincidence) than simply some observers making some mistakes.

 

[TheCholla]

I'm glad that we refined it to two possible solutions. I feel like we are close to solving the case for good.

To me, we are left with the choice between two extraordinary scenarios :

1) A distant unregistered plane that is mistaken as a U-shaped close trajectory by the pilots, with a wrong 6-8Nm range, weird "fleet of them" on the ASA. Creating a glare that has an intriguing shape, and seems to rotate along the U-turn of the 10Nm trajectory. That shows a slight lowering of the clouds in the FOV, as you would expect from an object climbing a bit. And other points I listed in my other thread.

2) An aircraft that makes an extraordinary maneuver, a vertical U-turn at very slow speed. But that also, as pointed out by Eddie, has a trajectory that corresponds to a straight line further away (kinda, as I have a reservation about this, but I don't want to go into this again). And yes with a speed consistent with a plane too (although it does for a large range of altitude along the lines of sight).

I think we can at least agree on the complexity of this, and respect each side's arguments.

Personally, I try to put myself in having to defend one or the other scenario.
Scenario 1, the fact that you need to appeal to technical glitch, or huge pilot errors, when all the direct data aligns with the trajectory they describe, is a hard pill to swallow.
Scenario 2 is basically making a very strong case for the existence of non-human aircrafts in our skies, which is a very hard pill to swallow too
(or possibly electronic warfare during Navy training, another theory defended here, but with very little evidence for it).

Occam's razor is difficult to apply with this case.

I think at this point we need experts to chime in, weapon system officers, Ryan Graves, ATLFIR experts. Only them can end this debate for good. They talk privately, but are very reluctant to go public or say things clearly, which is very frustrating.

 

[Edward Current]

To me, we are left with the choice between two extraordinary scenarios :

1) A distant unregistered plane that is mistaken as a U-shaped close trajectory by the pilots, with a wrong 6-8Nm range, weird "fleet of them" on the ASA. Creating a glare that has an intriguing shape, and seems to rotate along the U-turn of the 10Nm trajectory. That shows a slight lowering of the clouds in the FOV, as you would expect from an object climbing a bit. And other points I listed in my other thread.

2) An aircraft that makes an extraordinary maneuver, a vertical U-turn at very slow speed. But that also, as pointed out by Eddie, has a trajectory that corresponds to a straight line further away (kinda, as I have a reservation about this, but I don't want to go into this again). And yes with a speed consistent with a plane too (although it does for a large range of altitude along the lines of sight).

Scenario 1 isn't extraordinary. It's unexpected, and unlikely to occur on any given day, but not extraordinary, except through an appeal to incredulity. (I keep forgetting that Graves et al. suggest 6–8 NM. I've never done those scenarios, but they are going to be even weirder than at 10 NM, maybe even displaying measurable "snap," the 2nd derivative of acceleration.) [Edit: Struck. See below.]

I wouldn't say that the 10 NM maneuver, in and of itself, is extraordinary, either. There is no reason why that trajectory couldn't be reproduced with existing technology, if that's what someone wanted to do. It would take some work, but totally doable.

What is extraordinary is that there's a banal straight and level solution in the same subspace — that a straight and level path could have been followed, within a typical airspeed window of aircraft that very much exist, and the picture would be exactly the same. As Mick alluded above, we would expect this only if the craft were being maneuvered with the express intent (i.e., "what someone wanted to do") to appear like it might be moving in a straight line — but, only from the perspective of one particular F/A-18 taking one particular path, the craft-maneuverer seemingly having full knowledge of how that path will unfold in time, from the beginning.

That's extraordinary.

 

[Leonardo Cuellar]

Even in the case of a randomly generated, smoothly accelerating/jerking trajectory along some camera sightline derived from an arbitrary cloud motion, the corresponding straight and level solution (if any) might be hundreds of miles away. It might be behind the observer. It might require extraordinary speed.

This is the limit of your analysis

 

[TheCholla]

Scenario 1 isn't extraordinary. It's unexpected, and unlikely to occur on any given day, but not extraordinary, except through an appeal to incredulity. (I keep forgetting that Graves et al. suggest 6–8 NM. I've never done those scenarios, but they are going to be even weirder than at 10 NM, maybe even displaying measurable "snap," the 2nd derivative of acceleration.)

Note that he says that they ended up at a 6-8Nm distance from the object, "before too close for comfort in low visibility". At the beginning they are further away. Starting at 10Nm my trajectory ends at 7.5 Nm, in the range he gives.

What is extraordinary is that there's a banal straight and level solution in the same subspace — that a straight and level path could have been followed, within a typical airspeed window of aircraft that very much exist, and the picture would be exactly the same. As Mick alluded above, we would expect this only if the craft were being maneuvered with the express intent (i.e., "what someone wanted to do") to appear like it might be moving in a straight line — but, only from the perspective of one particular F/A-18 taking one particular path, the craft-maneuverer seemingly having full knowledge of how that path will unfold in time, from the beginning.

That's extraordinary.

Like I said above, how one interprets this is up to his/her own sensibility. We can reverse the problem the other way around, I find it extraordinary that the glare from a distant plane ticks all the boxes that a close object in a U-turn trajectory would do : rotation during the U-turn, no sign of plane even when rotating, gets bigger as expected from the object getting closer, gets a little higher in the FOV, has a well-defined and constant shape when seen under a similar angle at the end.
And all this from an unidentified plane flying at unusual altitude in an area of US Navy training, with other instruments in the F-18 seemingly pointing to a range within 10Nm. Plane seen from a roughly similar angle of incidence but that creates a glare that changes shape and gets significantly bigger, while the pod rotates in steps during the gimbal roll. Crazy stuff, at least to me.

I also find the second scenario extraordinary.

 

[DavidB66]

with other instruments in the F-18 seemingly pointing to a range within 10Nm.

I may have missed something, but I wasn't aware that any instruments in the F-18 gave an indication of range. The Situation Awareness display had data from other sources, which we haven't seen.

 

[TheCholla]

I may have missed something, but I wasn't aware that any instruments in the F-18 gave an indication of range. The Situation Awareness display had data from other sources, which we haven't seen.

I'm not going into this again. I said "F-18 seemingly pointing to a range within 10Nm", as confirmed by the weapon system officer who was in the F-18 during the encounter, and Ryan Graves on Twitter. The close-object scenario reflects the trajectory they describe, that the range they got was accurate or not. Feel free to embrace scenario #1, I'm not going to argue about this further, I made my point.

 

[jarlrmai]

Their statements do not seem to comport with reality and they never really started making these claims until the rotating etc was debunked.

 

[DavidB66]

I made my point

You referred to 'instruments in the F-18'. I asked what you meant. You haven't replied to that, so I don't think you have 'made your point'. It's not a trivial detail: if the F-18 had instruments on board which gave a range for the object, that's important, and more credible than the other systems which appeared to show a whole fleet of objects doing strange things.

 

[TheCholla]

What do you want me to say? I wasn't there in the plane, I don't know if instruments on board gave the range. But they say they had it, who else knows better than them.

When I say I made my point, it's about the original question Eddie asked : which scenario is the most likely? The discussion should maybe refocus on this.

 

[Mendel]

I wouldn't say that the 10 NM maneuver, in and of itself, is extraordinary, either. There is no reason why that trajectory couldn't be reproduced with existing technology, if that's what someone wanted to do. It would take some work, but totally doable.

Is this true, though?

Much of aviating is about energy management. If you want to land slowly on a runway (so that you can brake to a stop within its length), you need to start shedding altitude (potential energy) and speed (kinetic energy) early enough, or you're not going to be able to achieve this: there's only so much energy an aircraft can dissipate (or add) per second. Lose altitude, you'll speed up; gain altitude, you'll slow down, if you exceed those rates.

The 30 nm scenario, straight and level flight at constant speed, is neutral in terms of potential and kinetic energy, leaving only air resistance vs. thrust to consider, within a range that all jet aircraft are designed for.

The 10 nm U-manoeuver has fluctuating speed and altitude. With your simulation trajectory, if you have altitude and speed, you can compute the potential and kinetic energy that this craft would need to shed and pick up. If the total of this is near zero, we're going to be looking at something physical, something every aerobatic pilot at an air show routinely does: trading altitude for speed and vice versa. If the total is far from zero, we need to investigate which types of craft can lose energy that quickly, and pick it up as well, with only a marginally larger heat output to boot. It's at this point where your assertion, that "that trajectory [could] be reproduced with existing technology", may prove wrong. The energy analysis should show that.

 

[Edward Current]

Is this true, though?

I agree that an existing vehicle probably couldn't do it. But if you wanted to build something that could follow this trajectory, I think you could, with existing technology (multiple orientable jet engines of some kind, GPS, and a computer that controls the jets), and a lot of money and effort.

Most critically, though, you'd need advance knowledge of the trajectory needed to be followed. That's the most extraordinary aspect of this hypothesis, that such a trajectory allegedly was followed, when and where it did.

We're getting into semantics, but I would call the trajectory itself extraordinary if there were discontinuities or accelerations that could not be feasibly engineered using off-the-shelf technology.

 

[Mendel]

I would call the trajectory itself extraordinary if there were discontinuities or accelerations that could not be feasibly engineered using off-the-shelf technology

Yes.
My point is that we haven't done the analysis for this, and that this analysis ought to be include an energy analysis.

The two potential issues I see is

1. achieving sufficient deceleration;
2. cloaking the heat output from amplified acceleration.

Depending on the actual numbers, we might cross into "currently impossible" on these.

 

[jarlrmai]

@Mick West your tool is being used for misrepresentation over at Reddit again by the usual suspect.

 

[TheCholla]

@Mick West your tool is being used for misrepresentation over at Reddit again by the usual suspect.

I am the usual suspect, and I made a post about general conclusions from recent analyses of Gimbal (including mine). Because I think it's time to move the needle on this, in informing people how the data actually supports the official account from the Navy pilots.

I'm using Mick's simulator to test the scenario that I believe is the most credible, encouraging people to check it out and try for themselves. I'm not saying this is Mick's conclusion, or the only trajectory in his sim. The U-turn close trajectory has been found before Sitrec, Sitrec is just another corroboration it is in the lines of sight within 10Nm.

If you don't like it, propose a better and more credible scenario involving a distant plane.

 

[Woolery]

I'm not saying this is Mick's conclusion…

Just from reading your Reddit post, it isn't at all clear whether Mick West agrees with you or not. You do claim his reconstructions favor your conclusion. It also isn't clear from your post if there are other conclusions (such as any you do not favor) that might fit the reconstructions.

In your efforts to be objective, you might mention in your Reddit post that Mick strongly disagrees with you and link to his thoughts on what the reconstruction demonstrates.

 

[TheCholla]

Just from reading your Reddit post, it isn't at all clear whether Mick West agrees with you or not. You do claim his reconstructions favor your conclusion. It also isn't clear from your post if there are other conclusions (such as any you do not favor) that might fit the reconstructions.

In your efforts to be objective, you might mention in your Reddit post that Mick strongly disagrees with you and link to his thoughts on what the reconstruction demonstrates.

I have mentioned it already, but I added it more explicitly at the beginning of my main post.

The video I show is not using Mick's simulator, and I mention Sitrec for what it is, a publicly available tool to study Gimbal. I know it's under development, but it's been online for a month, and I don't see which modifications may completely change the lines of sight at close range. Especially because the close trajectories have been found in other models, it's a robust result.

 

[Edward Current]

One would think someone trying to create the impression of objectivity would at least mention the other popular scenario. Instead we get this:

Some people will search indefinitely for a more mundane explanation, because they cannot and will never accept the idea that this is an UAP.

Ignoring the fact that everyone agrees that this is a UAP…that is evangelist writing. I mean, it's fine to evangelize on Reddit, but in doing so, one loses any claim to objectivity.

This is how the situation can be presented objectively:

One result from my Gimbal simulation with clouds is that the object could have taken a straight and level trajectory at around 30 nautical miles. Another result is that it could have taken an increasingly upward, hook-shaped trajectory at 10 NM. Since I uploaded my video on the simulation, people have been arguing for one or the other on Twitter and in my DMs.

Some people are attracted to the 30 NM trajectory because it's minimally simple, like a jet would be flying. Others are attracted to the 10 NM scenario because it's closer to Lt. Ryan Graves' observation of (what he claims was) the Gimbal object coming to a stop and changing direction, inside of 10 NM, as seen on the situational awareness screen.

Meanwhile. . . .
Some people don't like the 30 NM scenario because either Graves would have to be mis-remembering the incident or lying, or the equipment would have to be malfunctioning, or misinterpreted by trained experts, for the object on the SA screen (with its attending "fleet") to be a more distant plane— and, that plane also was not identified as such at the time. On the other hand, some people don't like the 10 NM scenario because it's more like a 3rd-order math function than a physical trajectory of a real-world object.

I assume the 30 NM scenario has appears on Reddit previously, but I would ask, if you were completely new to this debate, just stumbling across it on Reddit, would you rather see both sides presented (followed by the writer's opinion/argument), or would you rather see the one individual's opinion presented as fact, as if there were no other position?

 

[TheCholla]

Yes, I am an evangelist now. Liar, pseudo-scientist, creationist, evangelist, ... keep the names coming, it doesn't matter.

Meanwhile we are making progress on reconciling the video with what Ryan Graves and the pilots report having seen.

About your last point, the glare/distant plane theory has been widely publicized, and has become the most recognized explanation for the event, in recent years. It's discussed in every Reddit post on Gimbal, including mine from yesterday. Don't worry, people know about it.

 

[Edward Current]

Yes, I am an evangelist now. Liar, pseudo-scientist, creationist, evangelist, ... keep the names coming, it doesn't matter.

I was referring to the writing, not you. But I can't stop you from self-identifying as such.

Meanwhile we are making progress on reconciling the video with what Ryan Graves and the pilots report having seen.

Did a new discovery occur? I think I'm the first person to have suggested that reconciliation, and it was months ago.

 

[Mendel]

Yes, I am an evangelist now. Liar, pseudo-scientist, creationist, evangelist, ... keep the names coming, it doesn't matter.

"Evangelist" is not an insult; in my understanding, it stands for someone aggressively pushing an idea, see e.g. "technology evangelist". It does not imply lying, pseudo-science, or actual religion, though it strongly suggests bias.

 

[TheCholla]

"Evangelist" is not an insult; in my understanding, it stands for someone aggressively pushing an idea, see e.g. "technology evangelist". It does not imply lying, pseudo-science, or actual religion, though it strongly suggests bias.

Just to clarify, I cited those because they are other names I received on Twitter. But we really don't care, back to topic.

 

[jarlrmai]

I agree. Similarly with the rotating glare observables, for it to be a weird 10NM trajectory, it would almost have to be a craft that is pretending to move in a normal manner, but only from the moving viewpoint of that one jet. This seems like an incredibly more complex assertion (or astounding coincidence) than simply some observers making some mistakes.

My main issue is the way the "unknown technology craft" story sort of evolves to fit the data uncovered by investigation by us.

You would think that any specific investigation done by the US Navy and AATIP etc would uncover this track and this amazing stuff (The craft appeared to pretend to be a jet moving on a straight line 30NM away) and that this would be THE story. But the orginal story (paraphreased) was

"Does this <gimbal.mp4> look like a jet? Nope"

Us after a few months work

"Well yeah, it does because of glare/rotating ATFLIR and parallax, see this math etc"

"Ah yeah exactly that's what we said, isn't amazing how it looks exactly like a jet but actually isn't"

The other issues are the UAP just coincidentally did this amazing feat just for the length of the clip in the video. I assume then for whatever reason breaking the charade so 'we' actually know it did it in the 1st place. given it was not visible?

I'm also a little unclear how, given we know that the UAP was only visible to the camera that 'we' know it was actually doing this? RADAR? But then if on RADAR why no SLAVE? (a question I've never got a good answer to)

 

[Ravi]

"Does this <gimbal.mp4> look like a jet? Nope"

Us after a few months work

"Well yeah, it does because of glare/rotating ATFLIR and parallax, see this math etc"

"Ah yeah exactly that's what we said, isn't amazing how it looks exactly like a jet but actually isn't"

I noticed this too. It is something that happens quite often in ufo cases (changing narrative).

 

[JMartJr]

And to give some credit where due, at least it shows a willingness to try to adapt theory to fit new evidence. The value of this is undercut if there is a predetermined line in the sand that cannot be crossed -- it CANNOT be just a distant jet -- but is at least WAY preferable to just claiming any new evidence as fake and chanting "Can't hear you, Sheeple," with fingers in ears.

(Sorry, been "debating" with a flat Earth proponent and am a bit raw around the edges, but a bit more primed to notice better behavior here and elsewhere.)

 

[Mendel]

And to give some credit where due, at least it shows a willingness to try to adapt theory to fit new evidence. The value of this is undercut if there is a predetermined line in the sand that cannot be crossed -- it CANNOT be just a distant jet -- but is at least WAY preferable to

It's still not a scientific process because falsification is ruled out either way.
They've just found a way to defend their belief whilst acknowledging the evidence; if they hadn't, they wouldn't.

That's why we can agree with them and say, we're probably never going to know what it is, so obviously it could be a flying saucer. But they won't agree with us that, since GIMBAL could just be a regular jet flying straight and level, GIMBAL can never be evidence of an alien spacecraft and discussing it further is therefore useless.

With FE, we have positive evidence of the shape of the Earth, so not acknowledging that is the only way forward for them. Instead, most FEers are happy to discuss observations close to water, which people like Heath Carmody have shown to be useless because refraction clode to water fluctuates a lot, sometimes even over the course of a few hours. These observations are as useless as fuzzy UFO pictures, yet they're what most of the discourse revolves around.

 

[FatPhil]

With FE, we have positive evidence of the shape of the Earth, so not acknowledging that is the only way forward for them. Instead, most FEers are happy to discuss observations close to water, which people like Heath Carmody have shown to be useless because refraction clode to water fluctuates a lot, sometimes even over the course of a few hours. These observations are as useless as fuzzy UFO pictures, yet they're what most of the discourse revolves around.

OT Tangent: Would an triangle of laser source and target both close to water across a bay (and in each other's drop - so an example of an FE "proof") observed by a third party, possibly elevated, out to one side be able to show that the laser beam was indeed bending due to refraction? I'm getting 101 here - if they don't believe the laser bends, why can't we just show them, from the side, that the laser bends? (OK, you might need some mid-way spray to explicitly demonstrate the beam's path, but that's just details.)

 

[Mendel]

OT Tangent: Would an triangle of laser source and target both close to water across a bay (and in each other's drop - so an example of an FE "proof") observed by a third party, possibly elevated, out to one side be able to show that the laser beam was indeed bending due to refraction?

The best way to show refraction is typically via background distortion, which is why Heath Carmody's observations at a mountain lake in the daytime are so useful: you can see the perceived water level go up and down while the mountainsides and-tops stay unmoved, so you see compression going on looking at the opposite shore, which means the light bends. Carmody also has a higher camera position that suffers less from distortion.

Single lasers don't show the geometry of the distortion, and if you run the experiment in the dark, you eliminate pretty much all external references, so you can claim what you want. (The oil rig "black swan" pictures were taken in the daytime, and the distortion is very obvious once you look for it.)

If you wanted to do a night light experiment, it'd be useful to move the laser vertically to quite some height and see if the observation is proportionate to the actual movement; when the light source and the camera are low enough so they should be obstructed by the curve under standard refraction, and they're not, moving the light vertically should reveal that it's in a distortion zone.

 

[DavidB66]

Would an triangle of laser source and target both close to water across a bay (and in each other's drop - so an example of an FE "proof") observed by a third party, possibly elevated, out to one side be able to show that the laser beam was indeed bending due to refraction? I'm getting 101 here - if they don't believe the laser bends, why can't we just show them, from the side, that the laser bends?

I think the practical problem with this is that atmospheric refraction is usually very slight, say not more than a few feet per mile. For example, in the Metabunk curve calculator, at a distance of 10 miles the difference between 'drop' with and without standard refraction is less than 10 feet. Viewed from the side, the average gradient of the curve would be only about 1 in 5000. Usually the bending of light due to refraction would be less than the curvature of the earth's surface itself, which is notoriously difficult to detect in a side view, even at Lake Pontchartrain.

The principle of refraction can be visually demonstrated by shining a laser through a denser medium, like water with a gradient of dissolved sugar or salt. Mick West did several experiments on this a few years ago. This video is possibly the clearest demonstration of the resulting 'curve':


Source: https://www.youtube.com/watch?v=oGMkIqAidK4&t=96s

 

[TheCholla]

I'm going to repost this message here, because I think it's an interesting question. We were debating with @Mendel about the distant flight path, and got there, but off-topic unfortunately. Now it's directly related to the question of this thread, about the probability of the distant versus close flight paths.

yes. because what we see is not the jet's signature, but an uneven glare that's distorting it, at a distance where a jet would rarely be locked

Now that's interesting. How did they lock onto this random distant plane, by the way? Do you realize how unlikely it is to find and lock on a random thing 35Nm away?

This is from the Raytheon documentation on the ATFLIR. The Palace of fine arts in San Francisco. Luckily it shows how ATFLIR see things from 38Nm away. It's NAR2 like in Gimbal, as suggested by the angular size analysis below, made by a user on Twitter.

Now picture a F-18 in there, it will be quite small (~3 times smaller than the palace). An illustration of the distance from where this scene would be shot :

So talking about probability, I'd like to hear what is the probability for the WSO to lock on a distant F-18 35Nm away, when he doesn't know it's there, just by accident. Even more a F-18 right behind bogus radar returns doing weird things on the SA at the same exact moment.

Unless the two are related. And then we go back to spoofing as the only explanation (or very weird instrument errors, but this is very unlikely too).

Or of course the object is at ~10Nm, and is the target they track on the SA.

 

[Mick West]

Do you realize how unlikely it is to find and lock on a random thing 35Nm away?

How unlikely? Compared to what? You can't just throw out vague uncertainties. Do some math.

Most distant planes are fairly close to the horizon from 25,000 feet. There's probably one or two planes nearby (how many?). WFOV is 6* FOV. The glare would be visible against the sky as a black dot in WFOV, and they could manually designate it. That's 6/360 = 1.7% of the horizon. So maybe 1 in 100 to 1 in 1000?

How often has this happened? How times has an ATFLIR been given a direction by radar? How do we even know what happened before the video clip? What happened after the clip? What does the SA page actually show, and how does this relate to this situation?

There are really far too many unknowns to really quantify this question, let alone eliminate the possibility, especially if we are to consider other possibilities of unknown probability, like anti-gravity or even aliens.

And the question of this thread is still if 30 NM is more or less likely than 10 NM, which has other factors than the ability to lock onto a distant object.

 

[TheCholla]

How unlikely? Compared to what? You can't just throw out vague uncertainties. Do some math.

Most distant planes are fairly close to the horizon from 25,000 feet. There's probably one or two planes nearby (how many?). WFOV is 6* FOV. The glare would be visible against the sky as a black dot in WFOV, and they could manually designate it. That's 6/360 = 1.7% of the horizon. So maybe 1 in 100 to 1 in 1000?

Why limit to the horizon? They could have looked at a large range of elevation if they were looking for their weird radar return. Most planes fly higher than 25000ft and would have been above them. You need a plane at 19000ft, which is not super common. How many planes fly at 19000ft, 300 miles off the coast? Put another factor ten to your probability?

The question is, how does that compare to two close curved path having a more or less straight projection further in the back? Difficult to quantify. The point is, the low likelihood of both scenarios has to be kept in mind.

How often has this happened? How times has an ATFLIR been given a direction by radar? How do we even know what happened before the video clip? What happened after the clip? What does the SA page actually show, and how does this relate to this situation?

That's all good questions, I'm glad you're asking. The thing is the aviators who were there know the answer to this, and they are 100% sure it wasn't a distant plane. Graves has no doubt and it seems he doesn't even want to reply to this kind of questions because he's had enough. The WSO testified in front of Senate staff members about it, reaffirming they had a stable radar track file, and that the object was at 6-8Nm at the end. They didn't get closer as they were afraid of collision. That's precise information they gave us, do what you want with it.

There are really far too many unknowns to really quantify this question, let alone eliminate the possibility, especially if we are to consider other possibilities of unknown probability, like anti-gravity or even aliens.

Tackling the problem with the idea that the close flight path is necessarily anti-gravity or aliens is not a good way to be objective, imho. Now, I make a friendly suggestion to add an option in Sitrec, to switch between a F-18 and a saucer-shaped object, so we could see how this shape look/behave along the different paths. It's your software and you're busy, so take it as what it is, a suggestion. I wish I could develop a 3D model like yours

 

[Mendel]

The question is, how does that compare to two close curved path having a more or less straight projection further in the back? Difficult to quantify. The point is, the low likelihood of both scenarios has to be kept in mind.

These likelihoods are not comparable.

If an observer does not lock onto anything with the ATFLIR, itt gets unreported, and never enters the statistics. So once we have a report, we are already limited to the "unlikely" cases of ATFLIR locking onto something, and then we also eliminate the multitude of close and well identifyable locks. The target might even have been too small, and identified as being too far away, to be worth considering if it hadn't been amplified by the glare.

So wondering why this is a rare situation is like wondering why all UFO reports are hard to identify: the reports that don't fit this criterium never make it to where we discuss them. Reality puts a filter in place that removes all of these more common occurrences (like not finding anything with ATFLIR) from our consideration.

But it doesn't work like that with the flight path. Most flying objects are traveling from A to B, efficiently, in a mostly straight line at a fixed speed, with short phases of changing altitude or direction. (The next big categories are wind-driven objects that depend on turbulence for their movement to be erratic, and otherwise move fairly straight as well.) So the straight path is already the likely one.

But the mathematical twist is that if you have video data of an object traveling along a random path from an observer travelling along a curved path, it is extremely unlikely that we'd be able to resolve it as moving along a straight path. So when we have a random path, we'd really expect mathematically to not be able to that. If we are able to do that for a path that isn't straight, something very unlikely is occurring. It's more reasonable to assume this path was straight to begin with.

What we do not have is a mechanism that lets us see only random paths that look straight. If the observing F-18 had flown any other way, that vertical-U-turn track could not be made to look straight. If that was indeed the UAP's track, wd hit upon a very rare set of circumstances that let us resolve it as a distant straight-flight object. And there's nothing that makes it more likely for us to see that sort of path.

On the other hand, if the UAP track was straight, it would always be resolvable as straight, no matter what the observer plane did.

So, the question is:
• are we looking at the rare occasion when a (rare) non-straight maneuver looks straight, or
• are we looking at the certainty of a (common) straight flight maneuver looks straight?

And there's just no equivalence to your observation that it's rare for ATFLIR to see something like it, where we don't ever need to consider the more common alternatives. With the flight path shape, there is no "reality filter" that works in favor of the rare occasion.

 

[TheCholla]

I understand your position, but like I said in the other thread, you're going all in with the distant projection giving a definite answer. Personally, with the witness accounts and SA data being left unexplained, and the very unclear set of circumstances for locking on a random plane at 35Nm (in NAR2 FOV), I would not bet my house on it.

I think we can agree that if this longer Gimbal video really exists, we need to see it.

 

[Edward Current]

Nobody's going all in or giving definite answers to anything.

 

[Mendel]

the very unclear set of circumstances for locking on a random plane at 35Nm

there is nothing unclear about it

we don't have a definite identification, but "jet traveling level & straight @ 30 nm" is by far the most likely, imo

 

[markus]

On the other thread, you said,

Just want to add that this extraordinary coincidence goes both ways : how could two fighter jets 35Nm apart, with one randomly flying away unidentified, move both in a way that mimics the close trajectory of a bogus radar return that stopped/reversed direction on the SA?
See, I cannot discard this piece of information that is central to this case. Graves and the aviators saw it very clearly from the velocity vector abruptly reversing direction on SA.

True, the ~straight/steady line (it's not obvious in Sitrec, I did not find it either, see below) is also a weird coincidence, but to go all in with it may be a mistake, imo. Because it's not clear as day, if you will.

(To see how the distant plane's speed needs to change in 15s: https://www.metabunk.org/threads/gimbal-3d-analysis.12303/post-267003)

The key part is this statement:

Just want to add that this extraordinary coincidence goes both ways

It doesn't. The coincidence goes one way only! The reason is simple: the vast majority of trajectories are not constant speed, constant altitude straight lines. Those trajectories have a small p value (how small depends on what how varied is the set of trajectories you're willing to consider). So when we see that the trajectory as seen from the observer is compatible with a straight line, that's unusual. That's why it would be a coincidence for a much closer object to be along a trajectory that happens to match what a straight line trajectory would look like from the vantage point of the F-18.

Now imagine the opposite, that an object moving in a straight line had its range misjudged, which led to the observer incorrectly assuming the trajectory is curved. Is it a coincidence that the trajectory is curved? No. Most trajectories are curved. In particular, if the distance were misjudged differently, the resulting trajectory would also be curved. It only appears straight (from a vantage point that's moving along a curve) if you get the distance right. So, how can it be a coincidence that a trajectory obtained from misjudging the distance looks like a trajectory with the distance misjudged?

Perhaps an analogy will help. Imagine you receive a deck of cards. You look through it and find that all the 52 cards are in order, A through K of Spades, A through K of Diamonds, K through A of Clubs, and K through A of Hearts. You may conclude this is a new deck, or at least that someone recently spent the time to sort it. Almost all the other 52! possible permutations are "out of order", so it would be a huge coincidence if the deck happened to be shuffled like this.

Now consider a different situation: the deck comes with the cards all scrambled, in, say, this order:

I would conclude from this that the deck has been shuffled. You might argue that the deck is new, likely the work of some avant-garde card company that eschewed the usual card order in favor of this one -- because it would be a huge coincidence, you might say, that the cards would come in this singular order.

But this order, of course, is not special -- it's just the one random.org happened to give.

Straight line trajectories are low entropy. Curved trajectories are high entropy.

 

[FatPhil]

Straight line trajectories are low entropy. Curved trajectories are high entropy.

Entropy can be a confusing concept sometimes (in particular when it was a new concept - it was roundly rejected), but the closely related concept of (Kolmogorov) complexity applies equally well.

Consider the following two strings of 32 lowercase letters and digits:

abababababababababababababababab , and
4c1j5b2p0cv4w1x8rx2y39umgw5q85s7

The first string has a short English-language description, namely "write ab 16 times", which consists of 17 characters. The second one has no obvious simple description (using the same character set) other than writing down the string itself, i.e., "write 4c1j5b2p0cv4w1x8rx2y39umgw5q85s7" which has 38 characters. Hence the operation of writing the first string can be said to have "less complexity" than writing the second.

-- https://en.wikipedia.org/wiki/Kolmogorov_complexity

 

[Mendel]

Entropy can be a confusing concept sometimes (in particular when it was a new concept - it was roundly rejected), but the closely related concept of (Kolmogorov) complexity applies equally well.

Consider the following two strings of 32 lowercase letters and digits:

abababababababababababababababab , and
4c1j5b2p0cv4w1x8rx2y39umgw5q85s7

The first string has a short English-language description, namely "write ab 16 times", which consists of 17 characters. The second one has no obvious simple description (using the same character set) other than writing down the string itself, i.e., "write 4c1j5b2p0cv4w1x8rx2y39umgw5q85s7" which has 38 characters. Hence the operation of writing the first string can be said to have "less complexity" than writing the second.

-- https://en.wikipedia.org/wiki/Kolmogorov_complexity

"write a random string"

the 30nm track can be described by a position and a velocity, i.e. 6 numbers; the 10 nm track needs its graph to describe it