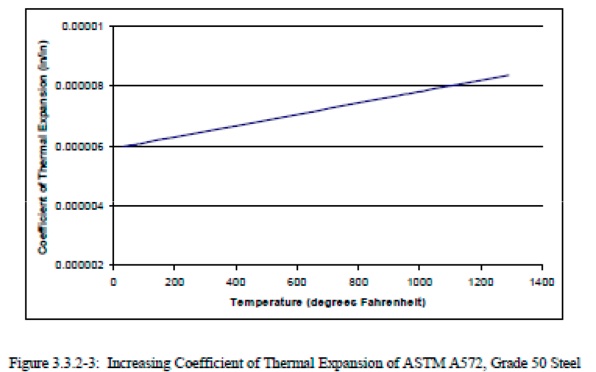
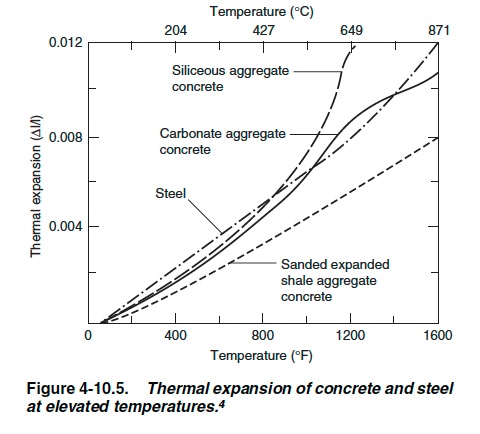
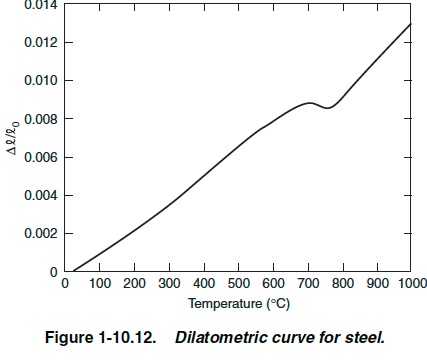
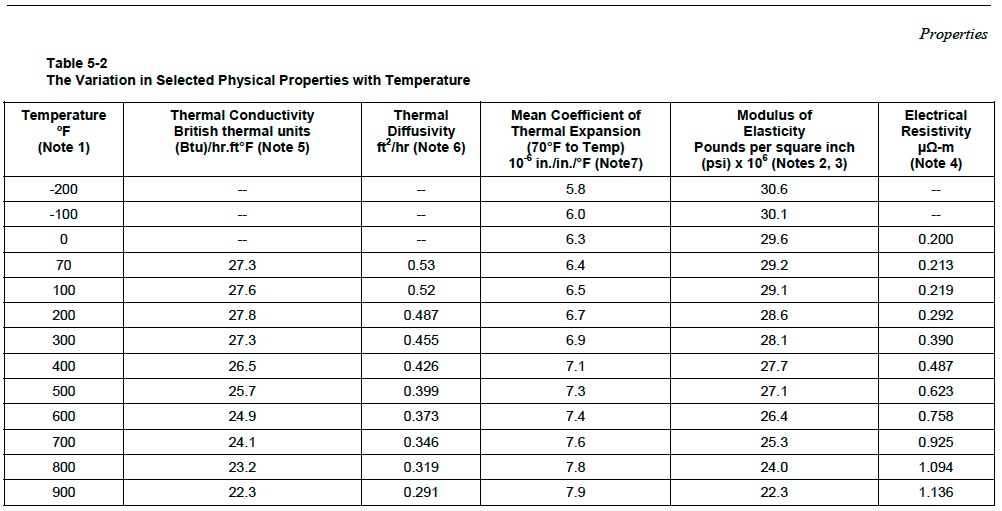
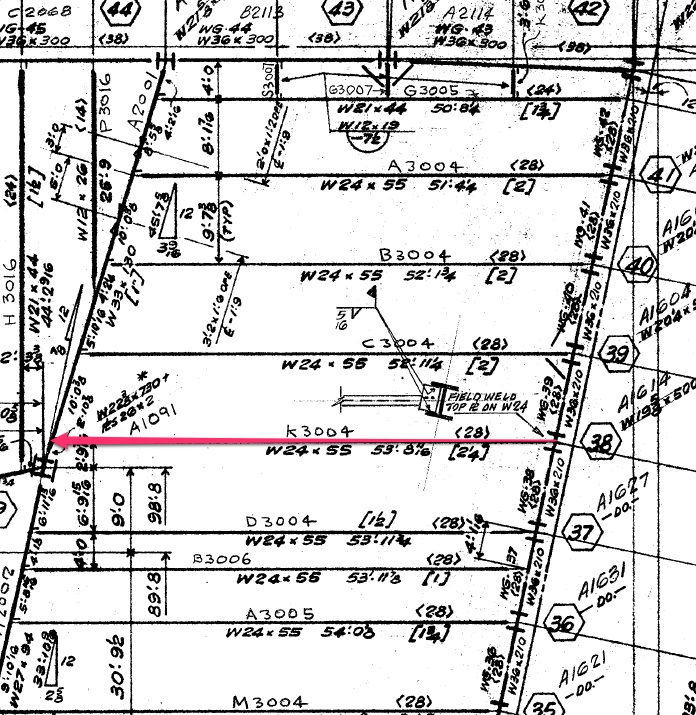
In World Trade Center 7, beam K3004 is thought to have expanded, and pushed Girder A2001 to the west. There is some dispute as to how much it could have expanded.
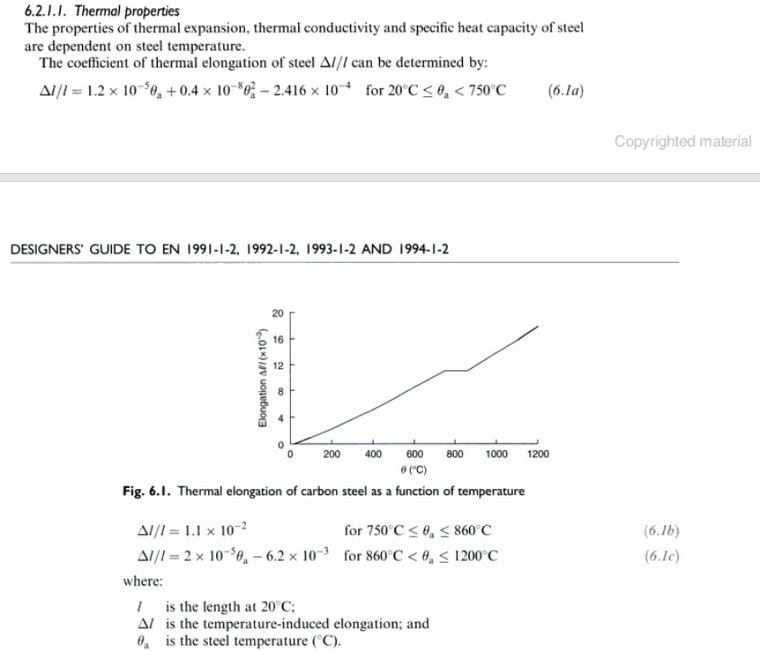
NIST NCSTAR 1-3E was focused on the WTC1/2 steel, however the findings regarding thermal expansion were carried over to the WTC7 investigation.


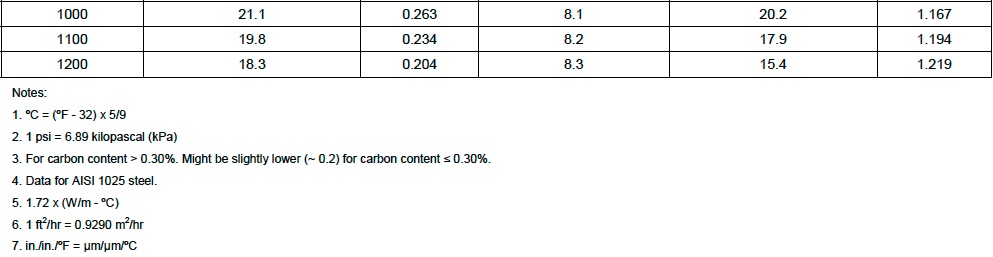
20C to 600C is 293K to 873K
Integrating the above polynomial over that range.
http://www.wolframalpha.com/input/?i=integrate (0.0000073633 +0.000000018723*x-0.0000000000098382*x^2+1.6718E-16*x^3) where x from 293 to 873
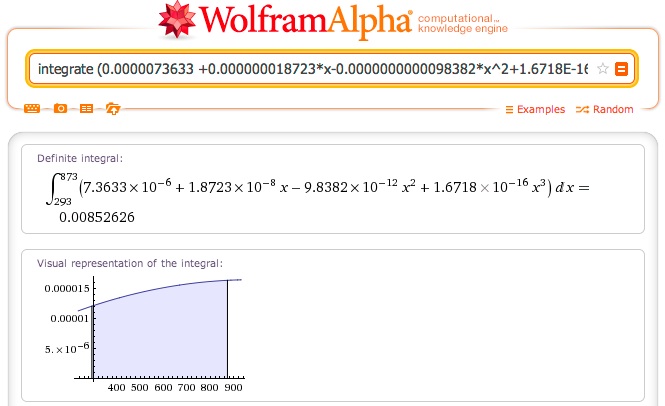
Gives 0.00852626, which we can multiply by the length of the girder, 53'8", or 644", to give 5.49"
NIST also gives the AISC recommendation:

Which is a straight line, but can still be simply integrated for convenience:
http://www.wolframalpha.com/input/?i=integrate (7.4954e-6 + 1.231e-8*x) where x from 293 to 873
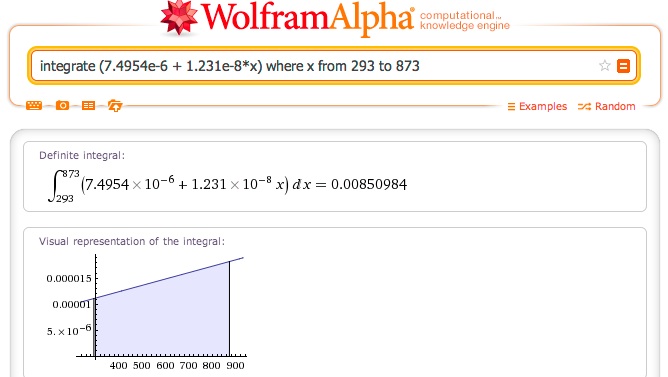
.00850984*644 is 5.48"
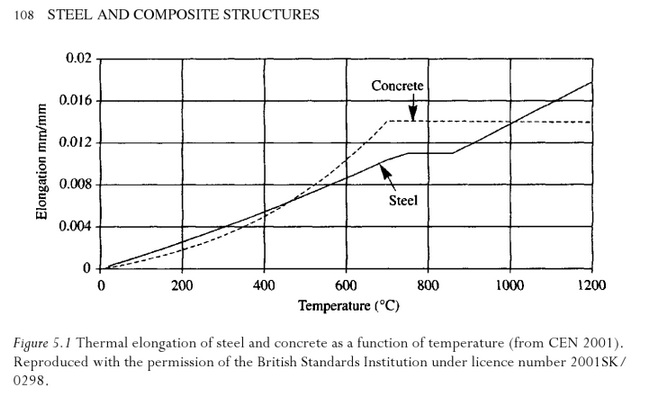
NIST also give the following chart of the expansion coefficient curves from various sources. The thick blue line is the polynomial used in the integration above, and the thick green is the AISC recommended value.
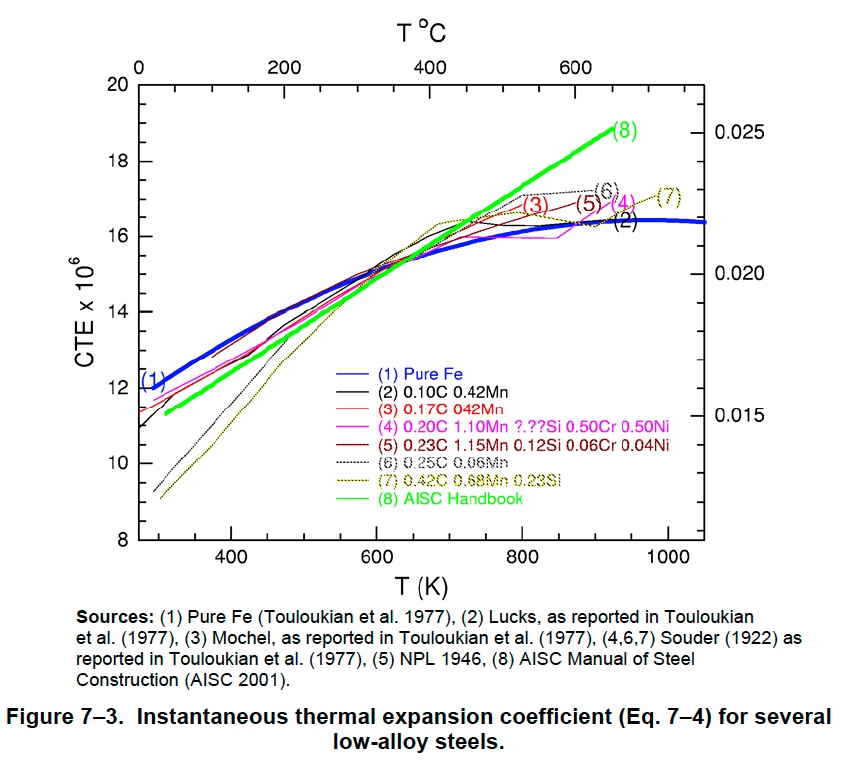
It's not entirely clear from the diagram, but it looks like some of those would give values slightly above 5.5"

NIST NCSTAR 1-3E was focused on the WTC1/2 steel, however the findings regarding thermal expansion were carried over to the WTC7 investigation.


20C to 600C is 293K to 873K
Integrating the above polynomial over that range.
http://www.wolframalpha.com/input/?i=integrate (0.0000073633 +0.000000018723*x-0.0000000000098382*x^2+1.6718E-16*x^3) where x from 293 to 873

Gives 0.00852626, which we can multiply by the length of the girder, 53'8", or 644", to give 5.49"
NIST also gives the AISC recommendation:

Which is a straight line, but can still be simply integrated for convenience:
http://www.wolframalpha.com/input/?i=integrate (7.4954e-6 + 1.231e-8*x) where x from 293 to 873

.00850984*644 is 5.48"
NIST also give the following chart of the expansion coefficient curves from various sources. The thick blue line is the polynomial used in the integration above, and the thick green is the AISC recommended value.

It's not entirely clear from the diagram, but it looks like some of those would give values slightly above 5.5"
Last edited: