StarGazer
Member
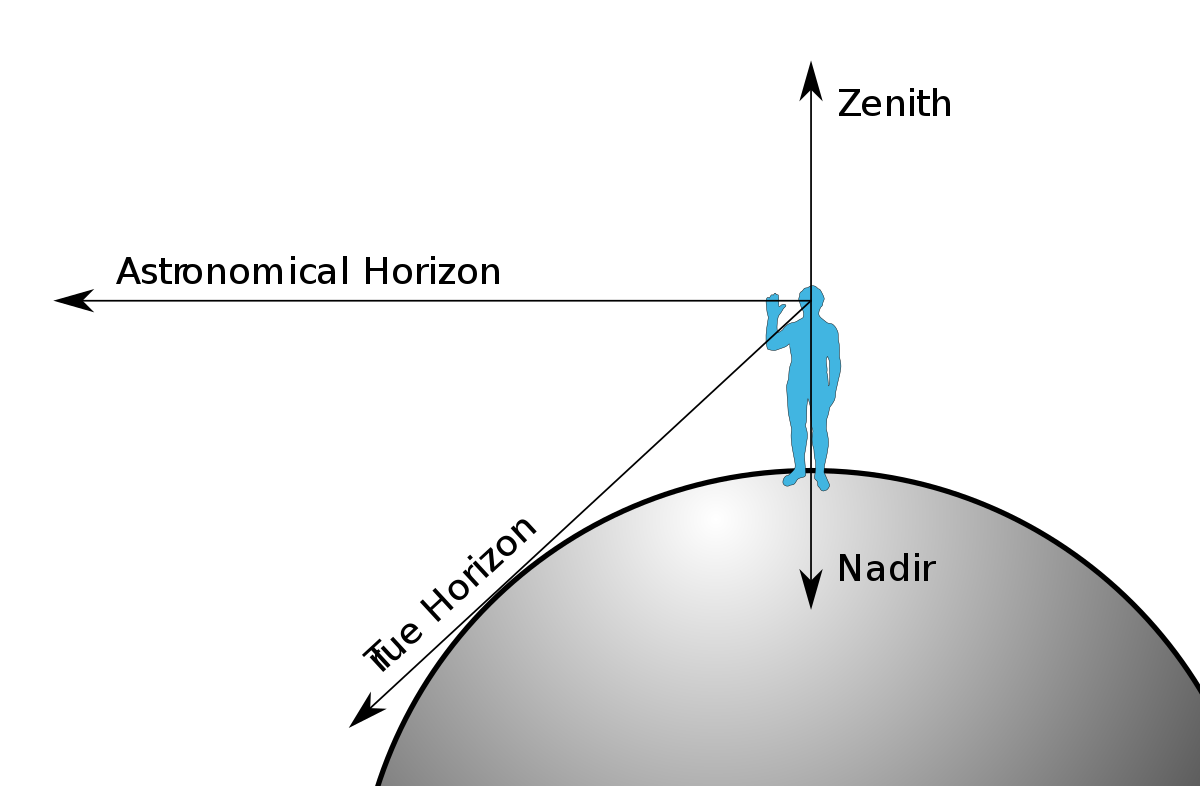
After reviewing my footage in more detail, I had the very strong sensation that between me and the lighthouse there was a wall of water much higher than my elevation.
Most noticeable after zooming out:
The distance from my position to the lighthouse was approx 18,11 km
My tripode + my camera were approx 1.5 m high.
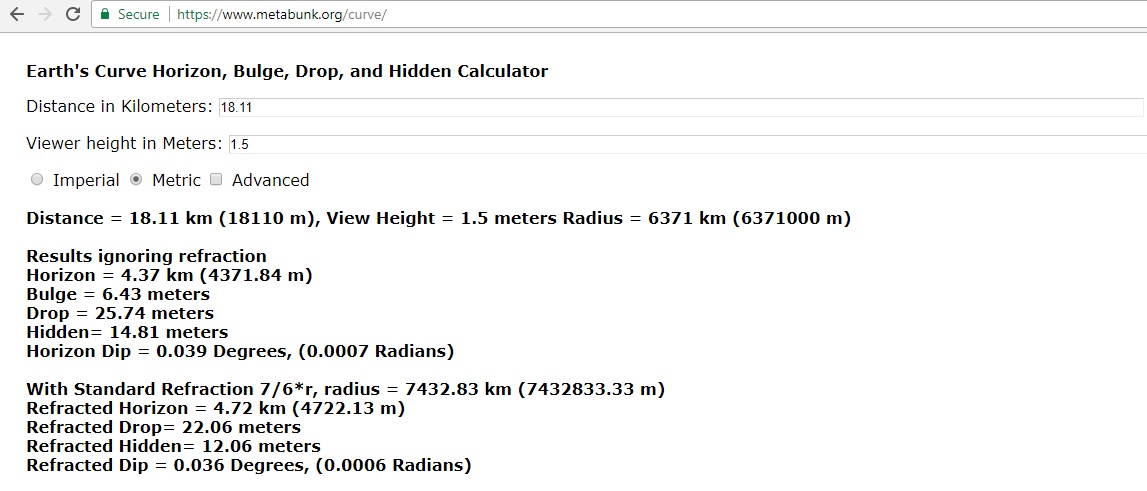
Since there are 14.81 meters hidden, without refraction, is it correct to say that on the straight line of sight midpoint between my camera's elevation and the lighthouse the sea's elevation is 14.81 meters? If not, what is the height?
Most noticeable after zooming out:
The distance from my position to the lighthouse was approx 18,11 km
My tripode + my camera were approx 1.5 m high.
Since there are 14.81 meters hidden, without refraction, is it correct to say that on the straight line of sight midpoint between my camera's elevation and the lighthouse the sea's elevation is 14.81 meters? If not, what is the height?