Sitrec - Metabunk's Situation Recreation Tool - Development Discussion

[Mick West]

Sitrec is a Situation Recreation tool that's just starting out in development. It's born from the Gimbal Simulator, and that's the only situation it's recreating - but eventually I'll extend it to GoFast, Nimitz, Aguadilla, Rubber Duck, mysterious DHS video #4, - and hopefully make it available so others can use it on arbitrary videos. You can see (and use) it here:
https://www.metabunk.org/sitrec/

The goal is to allow real-time analysis and visualization of the possible 3D interpretations that might fit a 2D video (and any other data for a particular case) and see from that what is the most likely scenario.

This is very much a work-in-progress, and not really usable for much right now, but I'm starting this discussion thread to track the progress and get feedback and ideas. The initial goal is to replicate and check the work of @Edward Current and his Blender simulation. https://www.metabunk.org/threads/gimbal-blender-simulation-with-clouds.12209/

 

[jarlrmai]

Be interested in how you maths adjustments for earth curve are implemented and whether you'll also use a refraction equation, I assume you have a lot of this work in the flat earth simulator code.

 

[flarkey]

Wow. This looks amazing. Would love to help with any Aguadilla investigation & simulation - i think my argument that the lines of sight from the camera all intersect along a straight line path (ie the path of the object) is pretty convincing. Perhaps that could be core principle of the simulation..?

 

[Mick West]

Wow. This looks amazing. Would love to help with any Aguadilla investigation & simulation - i think my argument that the lines of sight from the camera all intersect along a straight line path (ie the path of the object) is pretty convincing. Perhaps that could be core principle of the simulation..?

Yes, it's going to be fundamental. 2D -> 3D motion is largely about finding a path that matches lines of sight. Aguadilla is a great case with all the data that was extracted.

 

[Mick West]

Be interested in how you maths adjustments for earth curve are implemented and whether you'll also use a refraction equation, I assume you have a lot of this work in the flat earth simulator code.

Right now I'm use 7/6R for refraction, and the curve is just assuming a sphere. Some snippets

const EarthRadiusMiles = 3963 * 7/6

function drop(x,y,radius) {
    // dist = how far it is from 0,0 horizontally
    var dist = Math.sqrt(x*x + y*y);
    var drop = radius - Math.sqrt(radius*radius - dist*dist)
    return drop
}

// adjust z for curve of the earth
trackPoint.position.z -= drop(trackPoint.position.x,trackPoint.position.y,feetFromMiles(EarthRadiusMiles))

The track is currently calculated in local flat coordinate space (ENU, essentially), and then dropped down by the required curvature. Over these distances I don't think the difference would amount to much. Ideally though a full spherical (or WGS84 elliptical) flight sim model would be good - where the direction of gravity varies, and the pressure gradient is curved.

Merging in the ray-tracing from the refraction sim might happen eventually - but only if there's a case where it makes a difference.

 

[Mendel]

Pull data from the internet:
* ground elevation
* ground sat view (visible)
* clouds
* wind
* fire/lightning
* nearest METARs (aviation weather)
* plot a .kml flight path
* bright satellites/planets

 

[jarlrmai]

What are the tools/things we tend to do when investigating

Google Maps imagery and terrain elevation data
Placing 3d objects/cameras into scenes, usually phone cameras (28mm FF equivalent)
Placing, scaling photos in scenes as references
Aligning and overlaying other views in google maps
Street view (very handy)
Deriving ranges of object distances from estimated sizes in known cameras and vice versa
SteIllarium (usually we are looking for the Moon, Jupiter, Mars, Venus, Sirius, ISS + satellite DBs

Ideally some combination of Google Earth, Stellarium, ADSB exchange, simplified Blender and a flight sim like DCS/MSFS would be an amazing tool.

I know that's largely impossible without a big dev team and budget though.

 

[flarkey]

I think an achievable goal within budget could be the fusion of data that could make either or all...

1) the night sky
2) flight kml data
3) satellite pass data

... appear in the 'sky' part of Google Street view imagery. I've had to do this manually in the past with a copy and paste in MS-Paint. I'm sure there are better ways to do this.

 

[FatPhil]

I know that's largely impossible without a big dev team and budget though.

Does "Google Summer of Code" still exist? I wonder if they'd be sponsoring such an effort.

 

[jarlrmai]

@Mick West I know JS to a reasonable level if you need some legwork on the simpler things, however I also know it can be harder to set things up for collaborative development than to just solo it, but the offer is there if you need it.

 

[FatPhil]

@Mick West I know JS to a reasonable level if you need some legwork on the simpler things, however I also know it can be harder to set things up for collaborative development than to just solo it, but the offer is there if you need it.

You can do a lot worse than just having it in a github repo. Disciplined contributors, who can keep their patches to easily-reviewable changes, and their pull requests to rebased single features, are easy to manage. Rejecting a messy patchbomb that won't ff merge is a single click.

 

[captancourgette]

Looks sweet.
Minor observation with software, KISS, you're will be better off using metric internally, simplifies calculations and I assume most/all data you will pull from elsewhere esp if scientific will be in metric thus less prone to errors. And just display the final result in imperial if the user desires

 

[Mick West]

Some obscure complications with accounting for the curvature of the Earth. This might be an issue that others come up against.

The local environment (i.e. what Three.js renders) is stored as X,Y,Z, where Y is the up component, so the ground plane is X,Z. In geodesy this type of thing is referred to an ENU (East North Up) coordinate system (X = East, Y = North, , although unfortunately the three.js makes it EUS (East, Up, South).

This is a flat earth environment, so adjustments (i.e. the Z drop below the horizon plane) are made to the positions of things based on their distance in the X,Z plane from the origin. In Sitrec the jet starts at the origin

This works well for just position, rendering things like the clouds. The problem arises with a line of sight (LOS) at -2°. I was calculating this simply as 2° below the horizontal plane. However as you get further from the origin the horizontal plane tips. Not a lot, but for each mile it's 1/24901*360 = 0.0145°. Again, not a lot, until you remember that the entire video screen (in NAR 2x) is just 0.35°, so that's 4° of the screen, per mile.

So, we need to maintain an orientation frame for the local coordinates for any object, adjusted so that the local up is opposite gravity. Any LOS calculated from Az and El should then be transformed by this frame.

 

[Mick West]

While thinking about the above, I realized another complication. I'm using a world of radius 7/6 the radius of the earth, which is a simple way of accounting for refraction. This works in the sense that the horizon appears where it should when rendered, and a straight line of sight to the horizon (or the top of a cloud layer) will be at the correct angle.

However, I think this means that the direction of gravity is now slightly wrong, especially over longer distances. This could have an effect on the physics, which is obviously unaffected by refraction

So I think it might be better to simulate everything with the real radius, and just incorporate refraction in A) rendering from the pod camera perspective, and B) calculating lines of sight for display, which will now be slightly curved

 

[Mendel]

However, I think this means that the direction of gravity is now slightly wrong, especially over longer distances.

You mean it's no longer perpendicular to the surface?
(As long as you have that down, you're probably ok.)

There may be trouble with the larger radius when looking at orbital or astronomical objects, e.g. a skylink train or a sunset (or Venus).

 

[TheCholla]

The clouds in your simulation are impressively close from the real vid. This is an amazing tool. Is it ok to use it already? Or you are still going to make some changes?

I have tried to recreate our scenario with the object starting at ~10Nm, and setting Vc so the object is going on a vertical U-turn (straight/stop/reverse direction as seen from above). The trajectory looks like what I found in my model, and the object's rotation is a very good match with the U-turn.

As for now your sim seems to show exactly what we claim, that the close trajectories within 10Nm are very consistent with what R. Graves says.


Source: https://www.youtube.com/watch?v=wZdBGSNTXnQ

 

[Mick West]

Is it ok to use it already?

No, I'm still validating it, like with the issue above with local up (gravity) - something I've fixed (not deployed yet) but again illustrates the incredible sensitivity of the angles involved at this large distance.

I also need to have a variety of algorithms for traversing the LOS. Right now it just has constant distance + Vc. And probably wind.

As for now your sim seems to show exactly what we claim

Please don't represent this as me in any way agreeing with you. Right now this is an investigation tool, not a demonstration tool.

 

[TheCholla]

Please don't represent this as me in any way agreeing with you. Right now this is an investigation tool, not a demonstration tool.

Of course. I'll only use this tool to check our hypothesis, not to say you support it.

 

[Mick West]

Perhaps that could be core principle of the simulation..?

The basic paradigm of the tool is that it's node-based (in the sense of nodes on a DAG graph, not node.js), where a node is a data source and any node can have multiple inputs.

One node type is a traversal track, which takes a LOS track and some parameters, and then calculates a path from a start point that traverses the LOS.

Previously I just had one based on distance and closing velocity, but that's not really realistic, so I added one that is constant speed.

// attempt to traverse the LOS at constant speed
class CNodeLOSTraverseConstantSpeed extends CNode {
    constructor(v) {
        super(v);
        this.checkInputs(["LOS","startDistMiles", "speedMPH"])
        this.array=[]
        this.recalculate()
    }

    recalculate() {
        this.array=[];
        this.frames = this.inputs.LOS.frames
        let startDistance = feetFromMiles(this.inputs.startDistMiles.getValue(0))
        var position;
        for (var f = 0; f < this.frames; f++) {

            // how many feet do we want to move per frame?
            let perFrameMotion = feetFromMiles(this.inputs.speedMPH.getValue(f))/60/60/this.fps

            // flag to indicate if the target is moving away from the camera
            // if so then we pick the intersection that's further away
            let movingAway = perFrameMotion > 0;
            perFrameMotion = abs(perFrameMotion)

            const los = this.inputs.LOS.getValue(f)

            if (f === 0) {
                position = los.position.clone();
                let heading = los.heading.clone();
                heading.multiplyScalar(startDistance)
                position.add(heading)
            } else {
                let losPosition = los.position.clone();
                let losHeading = los.heading.clone()
                // we have a line from losPosition, heading vector losHeading
                // and a sphere at position, radius perFrameMotion
                // so find the intersections between the line and the sphere
                let ray = new THREE.Ray(losPosition,losHeading)
                let sphere = new THREE.Sphere(position, perFrameMotion)
                let target0 = V3() // first intersection
                let target1 = V3() // second intersection
                if (intersectSphere2(ray,sphere,target0,target1)) {
                    // hit the sphere, pick the near or far point
                    if (movingAway)
                        position = target1;
                    else
                        position = target0;
                } else {
                    // no intersection, so we use the same distance as the precious point
                    let oldDistance = los.position.distanceTo(position)
                    position = los.position.clone();
                    let heading = los.heading.clone();
                    heading.multiplyScalar(oldDistance)
                    position.add(heading)
                }

            }
            this.array.push({position: position})
        }

    }

    getValueFrame(f) {
        return this.array[f]
    }

}

This gets setup in the code like:

    // GIMBAL
LOSTraverse = new CNodeLOSTraverseConstantSpeed({
    inputs: {
        LOS: JetLOSNode,
        startDistMiles: new CNodeGUIValue({value: 30,start: 0.1,end: 50,step: 0.01,desc: "Object Start Distance"}, gui),
        speedMPH:  new CNodeGUIValue({value:380,start:-500,end:500,step:0.01,desc:"Object Speed MPH"},gui),
    },
})

Eventually, I want to have this all graphical, like the node editor in Blender.

But right now it's in code. Still, it's super flexible. I can just drop in new data sources or type of calculation.

Right now Sitrec is set up with the constant speed traversal, with a tweaked Azimuth curve to make it straight, starting 30 miles out, with a speed of 380 mph (got to switch to NM at some point)

Now there's an infinite number of solutions that fit along a LOS set, but a constant speed one is an obvious one to look at because it's a common occurrence.

If you reduce the start distance, the shape of the solution track gets curved, but only because the jet track is curved.

Like @Edward Current found, a distant straight-line solution will naturally appear curved closer to the jet

 

[Mick West]

Let's talk coordinate systems! (warning, super technical)

The Earth is, unfortunately, not flat. So we can't just use a simple x,y,z cartesian coordinate system. For simply designating a position there's Latitude, Longitude, Altitude (LLA) which is great for that, but horrible for doing math.

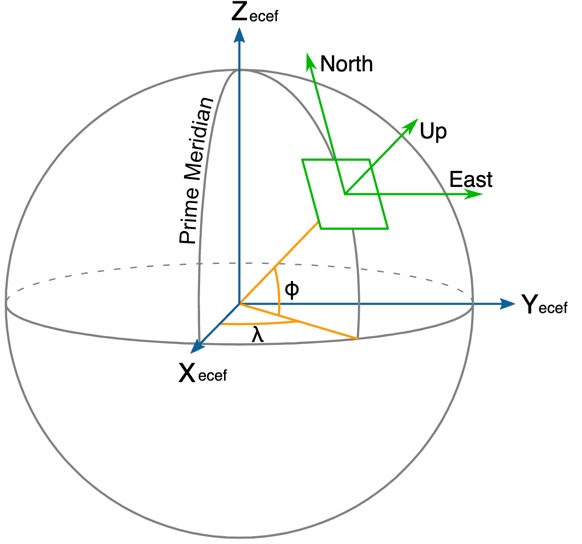
Then there's ECEF (Earth-Centered, Earth-Fixed), which puts the origin in the middle of the Earth and ignores rotation (of the Earth). That's usable, but everything ends up will really large numbers, as everything is so far away from the center of the Earth, and direction vectors are very unintuitive.

A happy medium is ENU (East, North, Up), aka "Local tangent plane coordinates" where you start from any given LLA position and then use x = East, y = North, and z = Up, where the x/y plane (the nearby ground, the green square in the image below) is assumed to be flat. This makes the math easy (North is just 0,1,0, instead of something like 0.23868293661, 0.234566334545, 0.9423423425) and this works just fine for anything under a mile.

ECEF, ENU, and LLA are shown here, the angles at the center represent latitude and longitude (altitude is not shown).

The 3D software I use for rendering on a web page, Three.js, has y=up, and z=south, so I'm using an EUS (East, Up, South) system, which is a bit of a pain as lots of library functions exist for LLA->ENU or ECEF->ENU. But ENU->EUS is a trivial operation.

So I use EUS, but with the curve of the Earth. This means the surface drops away from the x/z plane. It also means that things like a jet have to be reoriented for changes in local up (i.e. local gravity. So the jet has a local frame of reference (a rotation matrix) so that North (-z) and East (x) are parallel to the surface of the sphere, and Up (y) is perpendicular to it.

This is maintained when moving by a series of cross-products. In the simplest example:

    LocalFrame.matrix.extractBasis(_x, _y, _z)
    var localUp = getLocalUpVector(LocalFrame.position, jetAltitudeNode.v0, feetFromMiles(radiusNode.v0))
    _y.copy(localUp)
    _x.crossVectors(_y, _z)
    _z.crossVectors(_x, _y)
    var m = new THREE.Matrix4()
    m.makeBasis(_x, _y, _z)
    LocalFrame.quaternion.setFromRotationMatrix(m);

A frame of reference is actually stored as a quaternion, with a matching matrix. I take the matrix and devolve it into its basis vectors, then the up (y) vector is set to the worlds up vector at that point, in EUS coodinates.

Then _x.crossVectors(_y, _z) calculates East (x) as being perpendicular to Up and South
finally _z.crossVectors(_x, _y) calculates the new South (z) vector.

Then subsequent movement and calculation of lines of sight is in this frame of reference.

One additional complication is that I'm using 7/6 * radius of the earth, to simulate refraction.

 

[Mick West]

Some updates.
https://www.metabunk.org/sitrec/

• Added a "LOS Traversal Method" drop-down. This determines how we calculate the object path, currently one of two methods
  • Constant Speed - the default, maintains a constant speed - i.e. it moves the same distance between each LOS (line of sight) - at a rate of 30 LOS per second (29.97 actually). If the speed it too low for a segment of the path then that is show in RED and it switches to constant distance (at the same distance as the last good LOS) until it can do constant speed again. The start distance and speed are on sliders.
  • Constant Distant - just keeps the same distance from the jet. Probably the simplest, but not really making physical sense.
  • (TODO) need a "constant altitude"
  • eventually want a "solve for ..." a combination of parameters
• Added "Speed" and "Alt" (Altitude) graphs to show the per-frame speed and altitude of the target as you change various parameters.
• Added "el Rise" slider to determine the angular change (from the initial -2°) over the course of the video, allowing the target to rise a little above the horizon
• There's a variety of UI improvements and speedups that don't change the math.

 

[Mick West]

Updates:

• Fixed bug that was displaying the altitude graph incorrectly
• Added "Constant Altitude" LOS traversal method
• Moved the clouds back, so the area around the curves/lines is easier to see.
• Renamed "Constant Distance" to "Constant Vc", as that's what it actually is

 

[Mick West]

• Fixed inaccurate Three.js built-in line-sphere intersection resulting in inaccurate constant speed traversals at long distances.

 

[Mick West]

• Added a target object, a grey sphere with a user-defined diameter.

This is by default 37.5 feet in diameter. At 30 miles it's largely covered by the glare.

Skinny wingtips poking out would probably not be visible.

Closer up (8 miles here) the object would have to be quite a bit smaller (like <10 feet) to be obscured by the glare

 

[Mick West]

I've made a significant change to the Gimbal setting that removed a lot of manual fiddling.

The challenge was to replicate the cloud motion in the sim. Because of the large distance and narrow view angle, the cloud motion was super sensitive to both changes in azimuth and in turn rate. I was trying to tweak one and the other to make it work, but it was not really practical.

So I flipped the script, instead of editing the turn rate, I now calculate the turn rate from the cloud speed and the azimuth. The cloud speed is edited just to visually match the video (could probably be improved).

The results were revelatory! Even though I'm doing far LESS tweaking now, the result fit very nicely, and unexpectedly.

Here are the Azimuth and Cloud Speed editors. The blue line on the cloud speed editor is the turn rate (not to scale). Here the turn rate is derived from the smooth edited azimuth, so it looks smooth.

Now here's the same thing, but with the Az set to the extracted Az values from the video (Az Markus Smoothed), so again, less tweaking.

Notice two things. First, the graph on the left seems the same. The "Az Markus Smoothed" is within a pixel or so of the curve editor. Yet has a quite different result.

Second, the general shape of the blue line (turn rate) on the right is similar to before, now going down in more obvious steps, then back up again. The fun thing is that I did not add those steps. They simply arise from the AZ data and the cloud motion. Why significant? Compare to a turn rate "from bank and speed"

The blue line on the right is the calculated turn rate from bank angle and TAS (True Air Speed). Notice it has the same steps as the previous graph.

We can't use it as input, as it makes the cloud speed explode (the messy green line), but it does validate the turn rate extracted from the Az and the cloud speed. Quite a remarkable correlation.

 

[Mick West]

Removing all those sensitive tweaks and being purely data-driven also seems to smooth out the distant paths.

Here I'm using the recorded Az values, and we end up with a constant speed level flight in a straight line starting 45 miles away. If we solve for the most level flight, we get one at 53.6 miles away.

Still a work in progress, of course. But I think this is a very useful result - albeit yet another challenge in explanation.
https://www.metabunk.org/sitrec/

 

[Mick West]

Preliminary GoFast Situation.

https://www.metabunk.org/sitrec/?sit=gofast

A bit messy, as a lot of stuff is Gimbal specific. You'll want to change the LOS Traversal to "GoFast RNG value"

Note it includes the acquisition portion of the video, before about frame 400 - so that's a bit weird.

I think here again we'll want to drive the turn rate from the motion of the ocean (like we did with clouds in Gimbal), and not from raw bank+speed.

 

[Mick West]

Also the FOV is wrong, as is the target size.

 

[KalleMP]

Removing all those sensitive tweaks and being purely data-driven also seems to smooth out the distant paths. View attachment 50977

Here I'm using the recorded Az values, and we end up with a constant speed level flight in a straight line starting 45 miles away. If we solve for the most level flight, we get one at 53.6 miles away.

Still a work in progress, of course. But I think this is a very useful result - albeit yet another challenge in explanation.
https://www.metabunk.org/sitrec/

This is phenomenal and will probably become the go to tool for evaluating UFO and OTHER video footage from planes and drones as they start to diffuse into the social media sphere. You may find that the quality will approach that of professional simulators if you keep at it and air crash investigators (and those TV reenactments) will start to use it routinely simply as a tool to display black box data graphically.

I take my hats off to you for the coding skill and general determination to get this to work. While I can conceptually follow what you have done I cannot dream of achieving the same even with a team of skilled coders to try and help.

I think it would be great to test it on random out of the window videos of planes landing on those tricky runways on causeways and between buildings and mountains to see how well it can extract expected flight data from the terrain, very little gimbal tracking needed, a bit of hand shake to compensate for I suppose.

 

[Mick West]

I've added a first-pass FLIR1/Nimitz/Tic-Tac situation, so you can now do all three Navy videos:

https://www.metabunk.org/sitrec/?sit=gimbal
https://www.metabunk.org/sitrec/?sit=gofast
https://www.metabunk.org/sitrec/?sit=flir1

It's a bit fiddly, as some of the code is not working well with the upwards pointing LOS. Press the numpad "." key to reset the camera. Only "Constant Speed" LOS traversal works.

Without any real tweaking, it seems to support the general idea of a plane flying away and to the left. I smoothed out the Azimuth curve, and did a smoothly sloping Elevation curve (from 5.75° to 5°). Constant speed LOS traversal gives pretty much what I envisaged, with it being more tail-on at the start (hence the strong glare). Then the continued turn seems to match what is visible in TV mode.

 

[TheCholla]

What is a realistic altitude of flight for a plane (commercial, or F-18)? Because your FLIR1 sim can help refining potential distances for the object. It goes high very quickly with increasing distance, due to the 5deg elevation. At 30Nm, it's already around 43000 ft.
Is the 45000ft max altitude value on your graph, what you consider the max altitude a plane could be?

 

[Mick West]

What is a realistic altitude of flight for a plane (commercial, or F-18)? Because your FLIR1 sim can help refining potential distances for the object. It goes high very quickly with increasing distance, due to the 5deg elevation. At 30Nm, it's already around 43000 ft.
Is the 45000ft max altitude value on your graph, what you consider the max altitude a plane could be?

The default scenario is a 37.5ft wingspan object, at 35,500 feet, 15NM away, fairly constant distance. This fits an F/A-18

45,000 feet is higher than most commercial traffic, but not all. You can add a filter to Fr24 and there are about 40 or so, all business jets

This all really isn't new. Though, I think the size/distance estimates are consistent with what was calculated years ago. I've not checked in depth.

 

[gtoffo]

Just wanted to say this is really excellent work... nice job Mick.

 

[gtoffo]

The default scenario is a 37.5ft wingspan object, at 35,500 feet, 15NM away, fairly constant distance. This fits an F/A-18

45,000 feet is higher than most commercial traffic, but not all. You can add a filter to Fr24 and there are about 40 or so, all business jets

Just for reference: 45k feet is within the flight envelope of an F-18. But not comfortably.

You need full thrust (no afterburner) to stay in the air with a light load or afterburner with a heavy load. Min speed is 0.6 mach max speed is 1.5ish.
It would be great if SITREC included the F-18 flight envelope for reference so that some scenarios could be excluded.

If an F-18 can't fly it I would assume nobody else can.

 

[Mick West]

https://www.metabunk.org/sitrec/

Working on adding an SA page:

Fairly basic, but does show a simple "hafu" (the icon for Hostile, Ambiguous, Friendly, or Unknown Contacts) for the target, along with an aspect vector. Orientation is arbitrary, so the target is flying North in the close scenario.

This was prompted by a discussion with Ryan Graves about what the SA page actually looked like over the course of the encounter. I hope to add something like the "fleet".

Something that emerges is that for the close scenario it seems hard to determine from the SA exactly what is happening, and it's not clear how the entire fleet maneuver would be seen on this screen.

Click SCL to cycle through magnification scales.

 

[gtoffo]

https://www.metabunk.org/sitrec/

Working on adding an SA page:
View attachment 51394

Fairly basic, but does show a simple "hafu" (the icon for Hostile, Ambiguous, Friendly, or Unknown Contacts) for the target, along with an aspect vector. Orientation is arbitrary, so the target is flying North in the close scenario.

This was prompted by a discussion with Ryan Graves about what the SA page actually looked like over the course of the encounter. I hope to add something like the "fleet".

Something that emerges is that for the close scenario it seems hard to determine from the SA exactly what is happening, and it's not clear how the entire fleet maneuver would be seen on this screen.

Click SCL to cycle through magnification scales.

Really cool!

Not sure why you think it is hard to determine what is happening. The whole point of this page is to give Situational Awareness (SA) to the crew. You can even overlay the map over it if you want! Pretty cool. You see where everybody is, where they are going and who you are targeting. Also speed and angels (altitude) if you point one of the targets.

Observations:
1 nitpicky but the vector should originate from the border of the HAFU. Not the center.
2 in the video they say "there are all going against the wind." "The wind is at 120kts to the W".
Thanks to your tool we can figure out the direction they were flying towards in the various scenarios. Cool!
3 Can the clouds give us another tip regarding direction? This should be around dusk if I remember correctly but I would expect the illuminated part of the clouds to be slightly warmer. Or is altitude the only factor at night? In WHT hot we see that the base of the clouds is warmer. Could this mean that the sun just went down "behind" us?

 

[Mick West]

Not sure why you think it is hard to determine what is happening.

Well, I know what's happening (in the sim). The question is how Graves could have determined that the target moved in a straight line, and then back upon itself, just from looking at the video and the SA. Most of the movement on the SA screen comes from the rotation. We do see the aspect vector flip (should it also be shrinking?) But can you really determine from this that it's going in a straight line?

 

[Mendel]

Just for reference: 45k feet is within the flight envelope of an F-18. But not comfortably.

Article:

The B-52's service ceiling is officially listed as 50,000 feet, but operational experience shows this is difficult to reach when fully laden with bombs. According to one source: "The optimal altitude for a combat mission was around 43,000 feet, because to exceed that height would rapidly degrade the plane's range."

Source: https://en.m.wikipedia.org/wiki/Boeing_B-52_Stratofortress

Article:

On 22 March 2008, a Global Hawk set the endurance record for full-scale, operational uncrewed aircraft UAVs by flying for 33.1 hours at altitu des up to 60,000 feet over Edwards AFB.

Source: https://en.m.wikipedia.org/wiki/Northrop_Grumman_RQ-4_Global_Hawk

The RQ-180 might go higher than that. The SR-71 operated at 85k feet.

Cessna Citation X business jet:

Article:

Ceiling 51,000 ft (15,545 m)
Time to altitude 24 min to Flight level 470

Source: https://en.m.wikipedia.org/wiki/Cessna_Citation_X

 

[gtoffo]

Well, I know what's happening (in the sim). The question is how Graves could have determined that the target moved in a straight line, and then back upon itself, just from looking at the video and the SA. Most of the movement on the SA screen comes from the rotation. We do see the aspect vector flip (should it also be shrinking?) But can you really determine from this that it's going in a straight line?

View attachment 51396

Wow that flip is crazy. You can see the vector pointing consistently in the same direction basically. In your sim 340° of heading until the flip. So it's a straight line and then inverts direction.
The lenght of the vectors does not change as far as I know (in the old version of the HSI that the sims are based on - circa 30 years old). You get speed by selecting the target.

Remember that what we have simulations of is basically the old version of the Hornet. Current crews have new systems (probably similar?). For example this data would be projected in their helmets directly so they know where to look.

Article:

The B-52's service ceiling is officially listed as 50,000 feet, but operational experience shows this is difficult to reach when fully laden with bombs. According to one source: "The optimal altitude for a combat mission was around 43,000 feet, because to exceed that height would rapidly degrade the plane's range."

Source: https://en.m.wikipedia.org/wiki/Boeing_B-52_Stratofortress

Article:

On 22 March 2008, a Global Hawk set the endurance record for full-scale, operational uncrewed aircraft UAVs by flying for 33.1 hours at altitu des up to 60,000 feet over Edwards AFB.

Source: https://en.m.wikipedia.org/wiki/Northrop_Grumman_RQ-4_Global_Hawk

The RQ-180 might go higher than that. The SR-71 operated at 85k feet.

Cessna Citation X business jet:

Article:

Ceiling 51,000 ft (15,545 m)
Time to altitude 24 min to Flight level 470

Source: https://en.m.wikipedia.org/wiki/Cessna_Citation_X

All correct data points (RQ180 we have no idea). Bear in mind that an F-18 has a tiny wing span compared to most of those other examples.

At those altitudes the air is not very dense. You either need huge wings or huge speed.

The Cessna Citation X is a huge and powerful business jet. It has a Wingspan of 18meters and achieves max altitude at basically Mach 1.
B52 has 56meters of wingspan and also achieves max altitude at high subsonic speeds (and I presume low load).
The SR-71 is just on another scale but it would be moving at mach 4+ at those altitudes (no wings but huge engines - almost a rocket basically).

An F-18 is just not designed for this mission. It has other design goals (maneuverability, speed, load etc.)

 

[Mendel]

All correct data points (RQ180 we have no idea). Bear in mind that an F-18 has a tiny wing span compared to most of those other examples.

F18: 12m wing span, 37m² wing area, 45k ft.
Citation: 18m wing span, 49m² wing area, 51k ft.
GlobalHawk: 35m wing span, 50m² wing area, 60k ft.

I'm not confident that this would affect the IR profile much, especially from a horizontal
aspect; if you see the aircraft from below or above, they're obviously quite distinct. The point is, if all you have is a few pixels of glare, they're not that different, since the engines are close to the centerline. And it answers this:

What is a realistic altitude of flight for a plane (commercial, or F-18)?