How to calculate the visible fraction of the Earth [e.g. 1972 Blue Marble, Apollo 17]

[HoaxEye]

This question originates from a YouTube video called "NASA Blue Marble 100% Debunked" by Flat Earth Asshole (pardon the language, but that is their channel name).

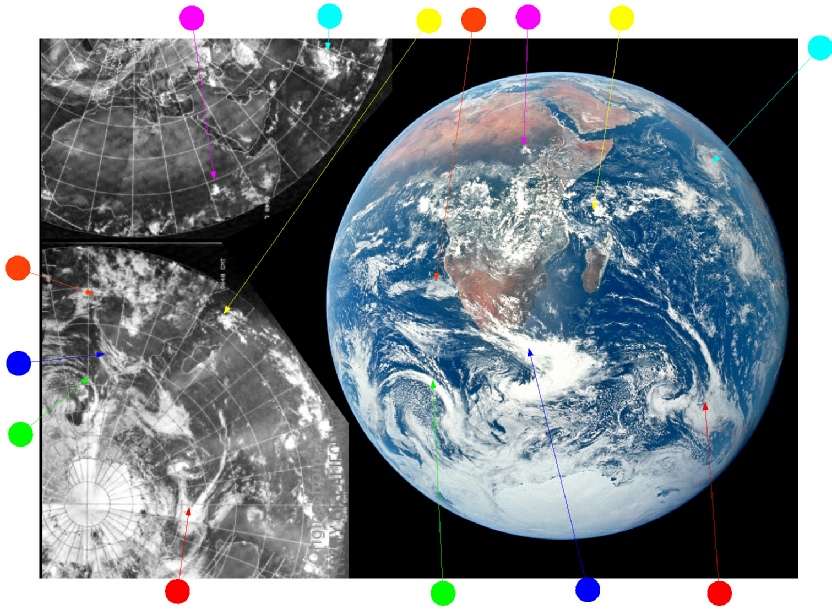
In the video, they make a claim that NASA's Blue Marble photograph from 1972 is a fake because it is not a correct representation of Earth: the areas that should be lit up such as Europe and South America, are on the other side of the Earth in darkness.

Link to the video Source: https://youtu.be/ZC8wYukRsdQ

Content from External Source

It is easy to counter the claim with a basic geometry fact: the "missing" land areas such as Europe and South America are hidden behind the horizon. You cannot get a full 180 degree view of the Earth from the distance of 45,000 km.

I could also use an example from Metabunk: Debunked: "Blue Marble" Photos show a Changing Earth https://www.metabunk.org/debunked-blue-marble-photos-show-a-changing-earth.t6616/ - the three photos of the household globe gives a good explanation.

But how to calculate the visible fraction of the Earth? I found a web tool that seems to do the job:

This program computes the visible fraction or illuminated fraction of the total surface area of a sphere at any distance from the eye or point light source as reckoned from the center or surface of the sphere.

Link: http://www.neoprogrammics.com/spheres/visible_fraction_of_surface.php

Content from External Source

With the distance of 45,000 km the tool gives a fraction of 0.43-0.44 - about 44% of the Earth. This sounds about right, but can I trust the math and calculations of this tool?

 

[Mick West]

can I trust the math and calculations of this tool?

Wolfram Alpha has some relevant math:
http://mathworld.wolfram.com/SphericalCap.html

The surface area of the spherical cap is given by the same equation as for a general zone:


Area of cap = PI*(a^2+h^2), where a is the radius of the cap, and h is the height of the cap.

 

[Trailblazer]

It's reasonably easy to determine how much of the Earth you can actually see in this picture and find whether that agrees with the illuminated part of the Earth at that time.

Photo is AS17-148-22725. High-res version here: Source: https://www.flickr.com/photos/projectapolloarchive/21692959852/sizes/o/


Close inspection shows that the terminator is actually just visible at the right hand edge; more easily seen if you overlay a circle on the image:



And comparing the position of the centre of the view here with the subsolar point (marked by the sun symbol on the map in the video, you can see that as expected the centre of the sunlit portion is off to the left of centre, i.e. the shadow terminator should be closer on the right side than on the left.



If you look very closely at the right edge of the Earth, you can see land in the sunlit region before you reach the terminator, which is in the correct place to be Malaysia:



And I think that further south you can just make out western Australia:




@One Big Monkey has a nice comparison of this image with satellite photography here:

http://onebigmonkey.com/apollo/CATM/ch4/a17/ch4_9_1a.html

 

[Trailblazer]

If someone has a globe to hand maybe they could recreate this photo? For a 12-inch globe you'd need to take the photo from about three and a half feet away.

 

[Henk001]

can I trust the math and calculations of this tool?

Yes. Here is a derivation of that formula using the formula and the symbols of the sperical map from Mikes post.

f is the fraction of the partial surface S of the total global surface A
According to the next picture

and using the uniformity of triangles you can derive

Insert this in the previous formula and you will find

 

[Mick West]

If someone has a globe to hand maybe they could recreate this photo? For a 12-inch globe you'd need to take the photo from about three and a half feet away.

9" Globe, 2' 6.5" from the surface.

And here's about 1' away:

 

[Trailblazer]

9" Globe, 2' 6.5" from the surface.

Not exactly the same angle but very close. And appears to confirm the ID of Malaysia and Australia at the right-hand edge.

[compare] [/compare]

 

[Trailblazer]

It's also interesting that the position of the centre of the view from Apollo 17 on the trans-lunar coast (i.e., on the way to the moon) almost exactly corresponds to the location of the moon's zenith on the map in the video (marked by the black circle). Fancy that!

 

[HoaxEye]

Many thanks to all of you! It is very much appreciated.

Also: I didn't want to start a "debunked"-thread, because I'm not sure if this video was made as a joke.

 

[Z.W. Wolf]

This seems to be what the author of the video is assuming: Since half the earth is sunlit, and I can see exactly half the earth, and everything in the photo is sunlit, I should be able to see everything on the Earth that is in daylight. If I can't see it, it's not in daylight.

But if you look at the photo it's easy to see that Europe is not in shadow, it's simply not present. So the problem simply goes back to perspective distortion. (You can't always see exactly half of a sphere.)

This video just adds another layer of assumption onto the perspective distortion problem which is: "I should be able to see half the Earth no matter how close or far I am from the surface."

The compound assumption is something like: Since I can see half the Earth and half the Earth is sunlit, and everything I can see in the photo is sunlit, anything I can't see in the photo isn't sunlit.

(Even though that would mean you would see a shadowed part of the Earth. The two assumptions aren't even compatible.)

 

[Trailblazer]

The compound assumption is something like: Since I can see half the Earth and half the Earth is sunlit, and everything I can see in the photo is sunlit, anything I can't see in the photo isn't sunlit.

(Even though that would mean you would see a shadowed part of the Earth. The two assumptions aren't even compatible.)

And. as I mentioned above, anything more than a cursory glance at the photo shows you that even part of the Earth that you *can* see isn't sunlit: the right-hand edge is in shadow.

 

[FlightMuj]

It's also interesting that the position of the centre of the view from Apollo 17 on the trans-lunar coast (i.e., on the way to the moon) almost exactly corresponds to the location of the moon's zenith on the map in the video (marked by the black circle). Fancy that!

But that is not the original picture, the original one is :Source: https://www.flickr.com/photos/projectapolloarchive/21692959852/

and the image of which's center you have taken is cropped, the center of the actual picture would not be that so how are you saying that they are headed in the direction of which's center matches where Moon is at Zenith? Or am I missing something?
Center by measurement is between the black circle:

 

[Mick West]

But that is not the original picture, the original one is :Source: https://www.flickr.com/photos/projectapolloarchive/21692959852/

and the image of which's center you have taken is cropped, the center of the actual picture would not be that so how are you saying that they are headed in the direction of which's center matches where Moon is at Zenith? Or am I missing something?
Center by measurement is between the black circle:

The center of the image is irrelevant. It's the camera's position in space relative to the earth and the sun that accounts for the position of the highlight. Moving the camera angle around a little to frame the shot differently makes no difference.

 

[FlightMuj]

The center of the image is irrelevant. It's the camera's position in space relative to the earth and the sun that accounts for the position of the highlight. Moving the camera angle around a little to frame the shot differently makes no difference.

Okay, so it means that where @Trailblazer marked the center of the Earth actually shows the cameras' position relative to Earth i.e. if we were to draw a straight line (shortest distance) to Earth it will fall to the place where Moon is at its Zenith?

 

[Mick West]

Okay, so it means that where @Trailblazer marked the center of the Earth actually shows the cameras' position relative to Earth i.e. if we were to draw a straight line (shortest distance) to Earth it will fall to the place where Moon is at its Zenith?

Kind of, it means he marked the center of the Earth from that point of view, and said "the center of the view". But there's really no such thing as the center of the view from a particular point in space. It varies based on where you point the camera, and how you crop the image. He really meant the center of the view of the Earth. The point here is that moon is above the center of the earth from the point of view of the camera, meaning the camera is nearly perfectly between the Earth and the Moon (assuming the time of the photo is correct).

So more illustratively. If someone in South Africa were to look 90° straight up a 10:40AM UTC, Dec 7 1972, then they would be looking straight at the moon, and at the spaceship. This would be spoilt somewhat by the moon being next to the sun and hence invisible.

 

[FlightMuj]

Kind of, it means he marked the center of the Earth from that point of view, and said "the center of the view". But there's really no such thing as the center of the view from a particular point in space. It varies based on where you point the camera, and how you crop the image. He really meant the center of the view of the Earth. The point here is that moon is above the center of the earth from the point of view of the camera, meaning the camera is nearly perfectly between the Earth and the Moon (assuming the time of the photo is correct).

So more illustratively. If someone in South Africa were to look 90° straight up a 10:40AM UTC, Dec 7 1972, then they would be looking straight at the moon, and at the spaceship. This would be spoilt somewhat by the moon being next to the sun and hence invisible.

I understand it know, but just to talk about a sense of Earth's curvature (a different visualization), If I were to make a line (from the perspective of the camera) and extend it to the place on Earth from where Moon is at its zenith that line will be the shortest distance and also perpendicular to the Earth's surface, right? Think about Earth's curve, it will be almost the shortest distance?
In other words from that place near Africa where Moon is directly overhead that line will be almost vertical i.e. 90° and the spaceship will be the nearest from anywhere on Earth.

 

[Mick West]

I understand it know, but just to talk about a sense of Earth's curvature (a different visualization), If I were to make a line (from the perspective of the camera) and extend it to the place on Earth from where Moon is at its zenith that line will be the shortest distance and also perpendicular to the Earth's surface, right? Think about Earth's curve, it will be almost the shortest distance?
In other words from that place near Africa where Moon is directly overhead that line will be almost vertical i.e. 90° and the spaceship will be the nearest from anywhere on Earth.

Yes. The middle of the visible disk of a sphere is always the closest point to the camera.

 

[FlightMuj]

I made a typo in my previous comment I actually meant:"...In other words from that place near Africa where Moon is directly overhead that line will be almost vertical i.e. 90° and the spaceship will be the nearest from the place we are looking which is on Earth.

Otherwise I am clarified on everything. Thanks!!!

 

[FatEarther]

A video from one of my favourite NASA paid shills explaining how much of the earth we can see at once (info relating to this thread starts at approx 19 mins into the video):

Source: https://www.youtube.com/watch?v=mxhxL1LzKww

 

[geoffrb]

[compare] [/compare][/QUOTE]

So we know that the whole of South America was illuminated (according to timeanddate.com), yet in the blue marble picture and this globe recreation, we can barely see a sliver of it?

 

[Mick West]

o we know that the whole of South America was illuminated (according to timeanddate.com), yet in the blue marble picture and this globe recreation, we can barely see a sliver of it?

Correct, this is because the camera is close to the globe, and so you can't see a full hemisphere. Which is what this thread is about.

Here's a similar view in Google Earth on Dec 7 with the sun in the same position.


View over South America


View over Australia:


The important thing to realize here is that when you are close to the globe you are seeing a lot less than half of it.

Read the full thread for more details.

 

[Z.W. Wolf]

The key to this is psychological. Break free of the feeling: "I can see the Earth as a ball surrounded by black space; so I can see half the Earth."


This satellite is far enough away that it could see the Earth as a ball, surrounded by blackness. But it's not far enough away to see half the Earth. It couldn't see the North Pole or the South Pole.

 

[Trailblazer]

This satellite is far enough away that it could see the Earth as a ball, surrounded by blackness. But it's not far enough away to see half the Earth. It couldn't see the North Pole or the South Pole.

The only limit, really, is how wide-angle your lens is. If you have a lens that can capture more than 180 degrees of view then you can see the Earth "as a ball" from the top of a tall building, and nobody would pretend that you can see the whole Earth, even from the top of the tallest building on the planet.



(That is a bit of a cheat as it is a stitched panorama to achieve the same effect as a very wide-angle fisheye lens, but the point remains.)

The further away from the Earth you get, the less of a wide angle you need to fit the visible portion of the Earth in the frame. But you can still only see as far as the horizon from that given height, which will never quite equal half the planet.

 

[MagnusE]

I have two questions. From this altitude do we expect atmospheric refraction to significantly increase the visible portion of Earth? And also, I have noticed that in both the blue marble and google earth the height of the earth (or the visible portion) is ever so slightly larger than the width. Is this due to geometry/ some perspective effect or something else?

 

[Clouds Givemethewillies]

H

(That is a bit of a cheat as it is a stitched panorama to achieve the same effect as a very wide-angle fisheye lens, but the point remains.)

How did you get up there to take the photos?

 

[DavidB66]

... I have noticed that in both the blue marble and google earth the height of the earth (or the visible portion) is ever so slightly larger than the width. Is this due to geometry/ some perspective effect or something else?

Could you say which images you are referring to? I checked the Google Earth image in post #21 above using my highly scientific measuring equipment (a ruler), and could not find any difference. (I mean the first image, in which the whole disk is illuminated, not the others, in which one side of the disk is in shadow.)

 

[MagnusE]

Could you say which images you are referring to? I checked the Google Earth image in post #21 above using my highly scientific measuring equipment (a ruler), and could not find any difference. (I mean the first image, in which the whole disk is illuminated, not the others, in which one side of the disk is in shadow.)

Figured it out. It's just the terminator line in the picture. I assumed it was completely sun-lit, but that was wrong. Look at the guy comparing it to a perfect circle. It is very slightly off.
Google earth is probably just my bad.

 

[Apollonius]

In Google Earth (at least in my version) you can't see more than about 40-45% of the Earth's surface at once. To confirm this, zoom out as far as possible and place one pole on the horizon. You won't be able to see the other pole. And if you center the image on one pole you won't be able to see the Equator.

This disposes of the argument that the heliocentric model is wrong because you can't see all the places illuminated by the sun at a given time in one Google Earth view. The images from the DSCOVR satellite, about a million miles in the direction of the sun, would be more likely to show all or nearly all places illuminated by the sun at a given time. Image 5 from this DSCOVR gallery approximates the Apollo 17 photo, but from much farther away:
epic.gsfc.nasa.gov/?date=2017-12-07

 

[Priyadi]

This has been making rounds in the past few days, with a new twist: they drew a circle on a map to indicate the visible area of Earth, but without accounting for the distortion of the map. And because the area outside the circle is much larger, they wrongly concluded that it must have been faked.



I made this map to illustrate the day-night areas of Earth along with the actual visible area of the Blue Marble image, using the same equirectangular projection used by time-and-date.com mentioned in the OP's video. The red area is the surface visible in the Blue Marble.



And this is how it looks on a globe:

 

[Vaeltaja]

I don't know if this helps at all with this, but here is a print screen from space engine with that date.