DavidB66
Senior Member.
I recently came across a flat earth argument about stars that was new to me, so it may be worth recording here.
I will try to present the argument as convincingly as I can.
According to standard scientific doctrine, the following points are true:
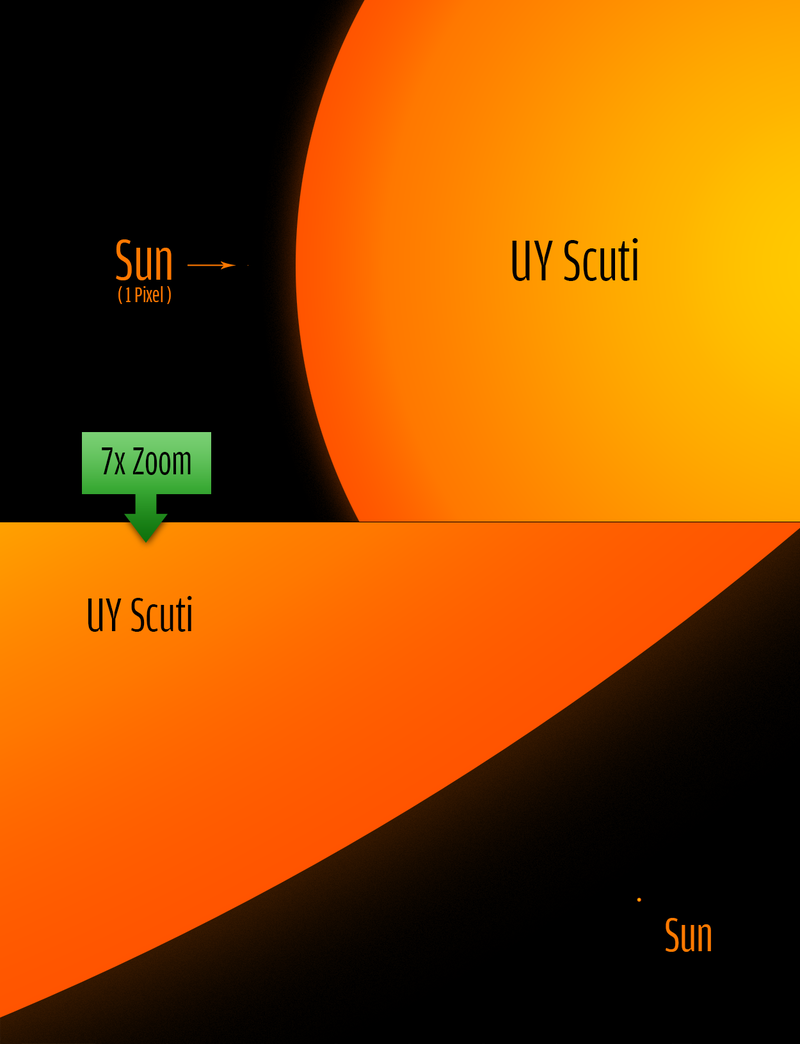
1. The sun is a star, and a fairly ordinary one at that.
2. The sun is about 93 million miles from earth.
3. The nearest stars (other than the sun) are over a light year from earth
4. A light year is about 6 million million miles, which is about 60,000 times the distance of the sun.
5. The nearest stars are therefore over 60,000 times as distant as the sun.
6. As viewed from earth, with the naked eye, the sun has a visual angle of about half a degree (30 minutes of arc.)
7. The visual angle of an object is inversely proportional to its distance from the observer.
8. At the distance of more than a light year, a star the size of the sun would have a visual angle of about 1/120,000 degrees of arc, or 1/2000 minutes.
9. But the smallest visual angle the human eye can resolve is about 1 minute of arc, which is about 2000 times larger than the angle derived at (8).
10. Therefore stars the size of the sun, or even much bigger, would not be visible to the naked eye from earth.
Since we evidently can see stars, the inference is that something must be wrong with the standard doctrine. Either the sun is not an ordinary star, or the sun is not 93 million miles away, or the stars are not light years away. ( I suppose in principle one might argue that the stars we can see are just those that happen to be much larger than the sun, but I wouldn't want to go down that road!)
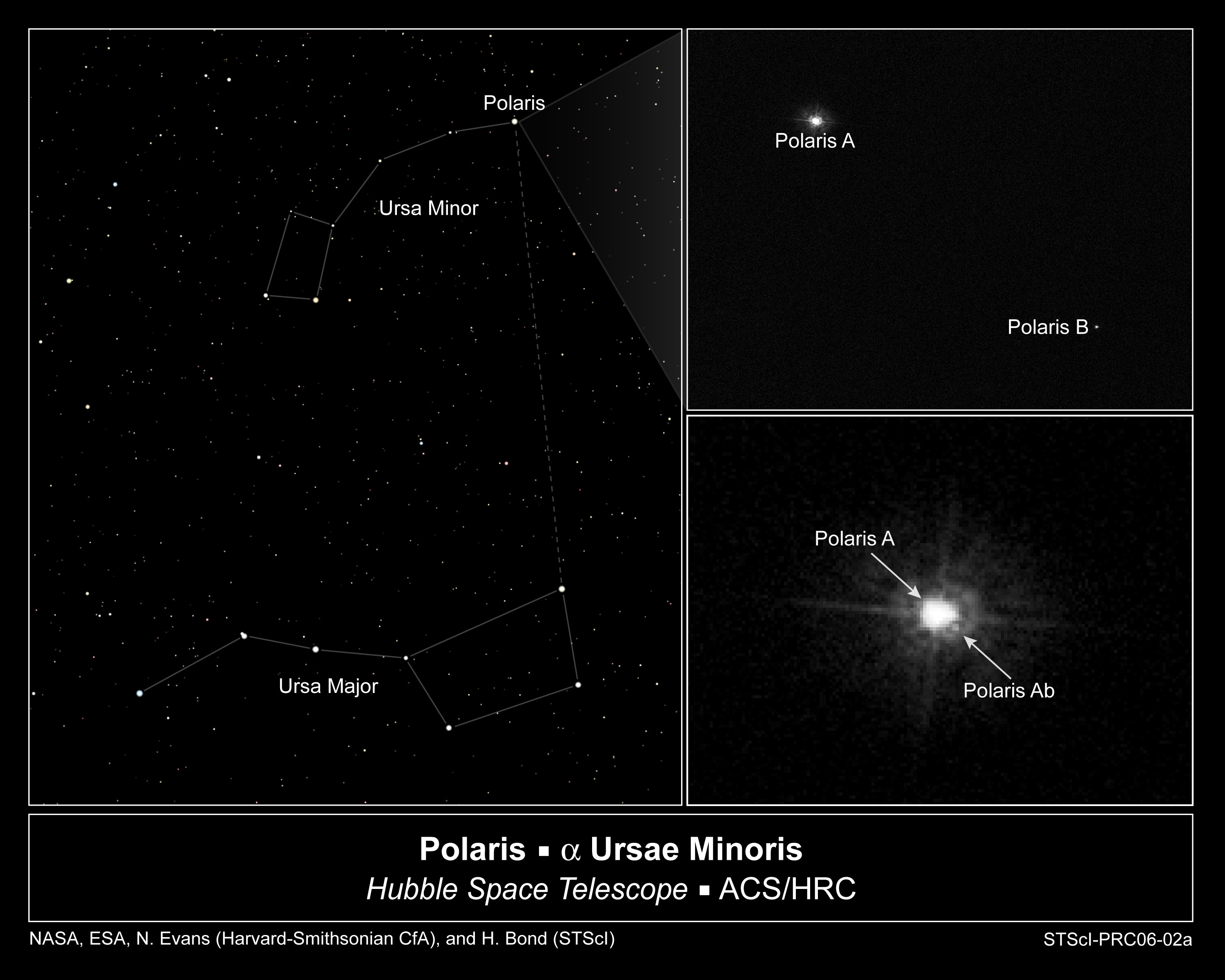
I presume the correct response to the argument is that it confuses visibility with having a definite visual arc. Points 1-9 in the argument are correct, but the conclusion at point 10 is invalid. In astronomy texts the stars are usually described as point sources of light, having no definite angular size, even when seen through a powerful telescope. Even at a distance of light years, they may still emit enough light to register on the retina (or other sensor) as a point of light. Some stars appear brighter than others, but this depends on the amount of light emitted, not their size. The same principle presumably applies to other light sources; for example, at a distance of 2 miles, a bright street light would have less than 1 minute of visual arc, but still be clearly visible. (I think.)
A more sophisticated answer would probably go into the number of photons emitted by a star; how many photons are needed to form a point image; and so on, but I hope I have got a valid answer in principle.
I will try to present the argument as convincingly as I can.
According to standard scientific doctrine, the following points are true:
1. The sun is a star, and a fairly ordinary one at that.
2. The sun is about 93 million miles from earth.
3. The nearest stars (other than the sun) are over a light year from earth
4. A light year is about 6 million million miles, which is about 60,000 times the distance of the sun.
5. The nearest stars are therefore over 60,000 times as distant as the sun.
6. As viewed from earth, with the naked eye, the sun has a visual angle of about half a degree (30 minutes of arc.)
7. The visual angle of an object is inversely proportional to its distance from the observer.
8. At the distance of more than a light year, a star the size of the sun would have a visual angle of about 1/120,000 degrees of arc, or 1/2000 minutes.
9. But the smallest visual angle the human eye can resolve is about 1 minute of arc, which is about 2000 times larger than the angle derived at (8).
10. Therefore stars the size of the sun, or even much bigger, would not be visible to the naked eye from earth.
Since we evidently can see stars, the inference is that something must be wrong with the standard doctrine. Either the sun is not an ordinary star, or the sun is not 93 million miles away, or the stars are not light years away. ( I suppose in principle one might argue that the stars we can see are just those that happen to be much larger than the sun, but I wouldn't want to go down that road!)
I presume the correct response to the argument is that it confuses visibility with having a definite visual arc. Points 1-9 in the argument are correct, but the conclusion at point 10 is invalid. In astronomy texts the stars are usually described as point sources of light, having no definite angular size, even when seen through a powerful telescope. Even at a distance of light years, they may still emit enough light to register on the retina (or other sensor) as a point of light. Some stars appear brighter than others, but this depends on the amount of light emitted, not their size. The same principle presumably applies to other light sources; for example, at a distance of 2 miles, a bright street light would have less than 1 minute of visual arc, but still be clearly visible. (I think.)
A more sophisticated answer would probably go into the number of photons emitted by a star; how many photons are needed to form a point image; and so on, but I hope I have got a valid answer in principle.