Alec Riz
New Member
When researching Flat Earth Theory there is 1 claim that I am finding puzzlingly hard to debunk.
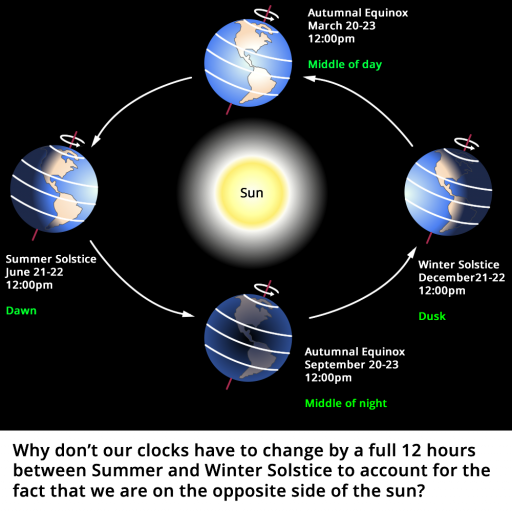
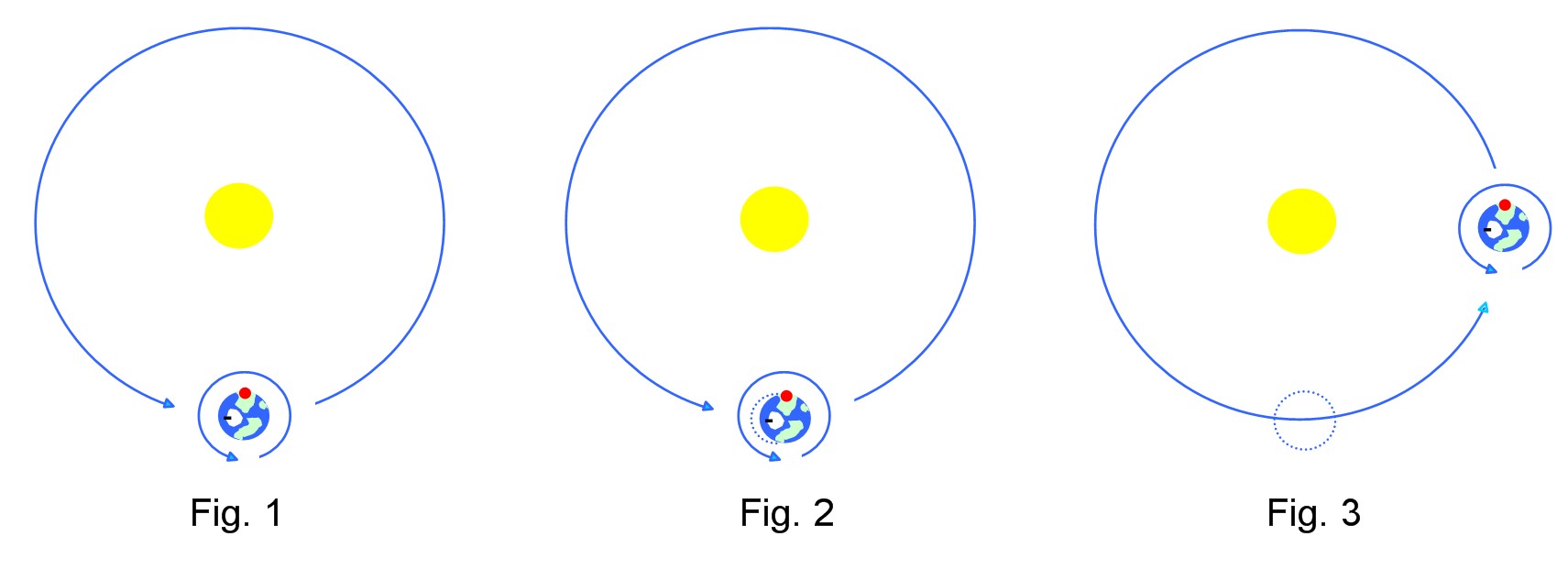
If the earth is spinning around its own axis, and orbiting around the sun, at a regular speed then, why don't we have to change our clocks by a full 12 hours every 6 months to account for the fact that we are on opposite sides of the sun.
For example - 2pm on Summer Solstice should be middle of the day which follows that if we are on the opposite side of the sun with both orbit and spin of the earth being consistent then 2pm on Winter solstice should be the middle of the night, but in actuality we only need to adjust our clocks by one hour.
Is there an obvious reason for this that I am missing??
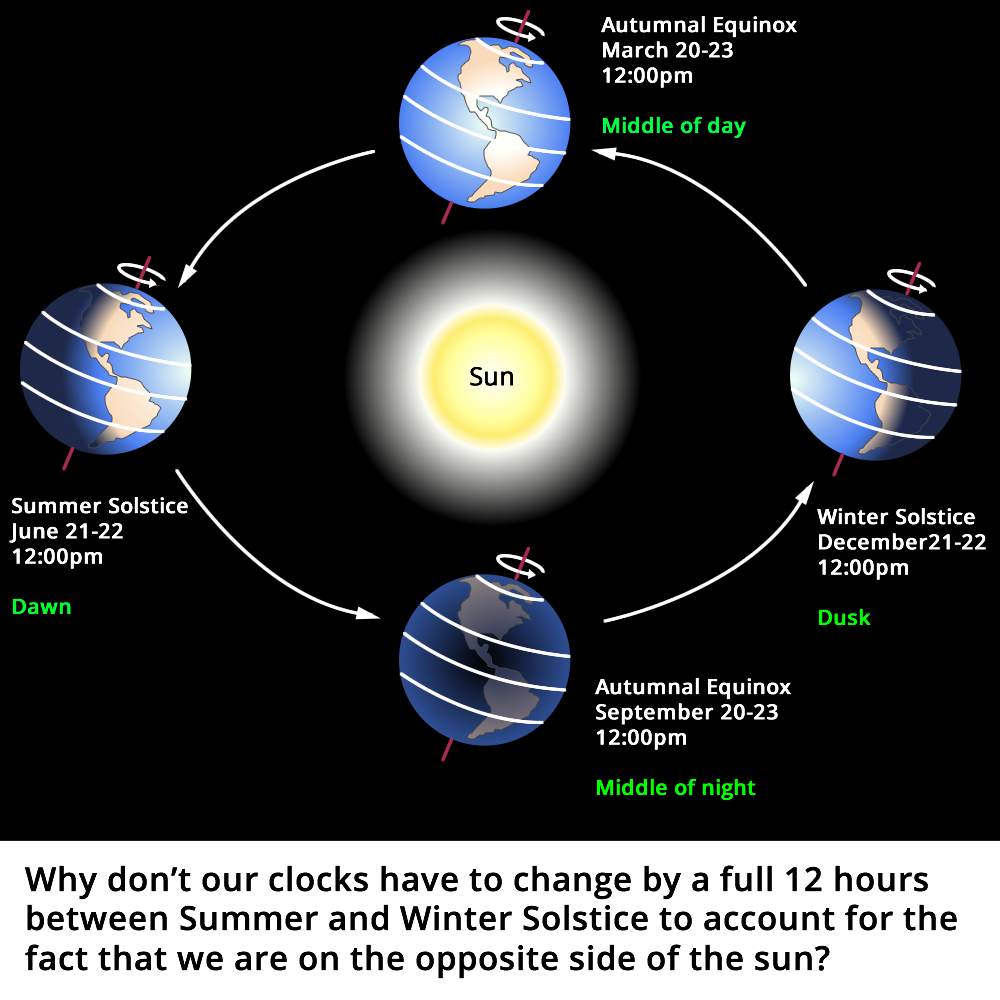
If the earth is spinning around its own axis, and orbiting around the sun, at a regular speed then, why don't we have to change our clocks by a full 12 hours every 6 months to account for the fact that we are on opposite sides of the sun.
For example - 2pm on Summer Solstice should be middle of the day which follows that if we are on the opposite side of the sun with both orbit and spin of the earth being consistent then 2pm on Winter solstice should be the middle of the night, but in actuality we only need to adjust our clocks by one hour.
Is there an obvious reason for this that I am missing??