CbIncus
Member
It seems to me that I've discovered some important errors in Carnicom's article "Halo Measurements": http://www.carnicominstitute.org/articles/halo1.htm. It states:
1. Carnicom calculates the angular dimensions of a 22-deg. halo with A = 360 deg/6 (hexagonal prism) and n = 1.31.
The equations are correct, but the result is valid only for the middle of the visible spectrum. Later he measures distance at the photos between the center of the sun and inner part of halo ring. This means that n refraction index should be changed to 1.3072 (red part of the visible spectrum). The D angle now becomes 21 deg. 37 min. 37.77 sec.
2. There should be a mistake in the calculations of the absolute error in D = (d / 21cm) * 2arctan(5.25/f) with errors of deltad = 0.08 cm and deltaf = 0.3 cm. We'll use the Lagrange formula for obtaining this result:
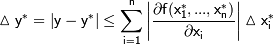
Partial derivatives (D in degrees):
a) for d: f(d) = d/21*2*arctg(5.25/16.7) = 1.662061807*d. The partial derivative is 1.662061807 and the part of absolute error 1.662061807*0.08 = 0.1329649446 (degrees).
b) for f: f(f) = 12.8/21*2*arctg(5.25/f) = 1.219047619*arctg(5.25/f). The partial derivative in radians is -20479954636/(3199992912*f^2+88199804637) (computed with http://www.numberempire.com/). Substituting f = 16.7 gives us -0.0208842 (the absolute value is 0.0208842) and the absolute error = 0.0208842*0.3 = 6.26526e-3. In degrees this is 0.3589729556.
Total error is 0.1329649446+0.3589729556 = 0.4919379 (degrees) = 0 deg. 29 min. 30.98 sec.
The real value of D computed by Carnicom is 21 deg. 16 min. +- 0 deg. 29 min. 30.98 sec. The precomputed value of 21 deg. 37 min. 37.77 sec is within the error margin.
I'm interested if some errors exist in my computations.
If measurements indicate a deviation from that result, it
informs us that the materials forming the
aircraft-generated halos, cirrus and cirro-stratus cloud
decks are no longer composed solely of ice as is often
claimed. The measurements do indicate such a deviation. Initial
halo measurements suggest that the hexagonal prisms of
uniform size and associated cirrus and cirro-stratus cloud
decks are not composed solely of ice as is usually
claimed.
1. Carnicom calculates the angular dimensions of a 22-deg. halo with A = 360 deg/6 (hexagonal prism) and n = 1.31.
D = 2 [arcsin(nsin1/2A)]-A or D = 21deg. 50min. 30”sec.
The equations are correct, but the result is valid only for the middle of the visible spectrum. Later he measures distance at the photos between the center of the sun and inner part of halo ring. This means that n refraction index should be changed to 1.3072 (red part of the visible spectrum). The D angle now becomes 21 deg. 37 min. 37.77 sec.
2. There should be a mistake in the calculations of the absolute error in D = (d / 21cm) * 2arctan(5.25/f) with errors of deltad = 0.08 cm and deltaf = 0.3 cm. We'll use the Lagrange formula for obtaining this result:
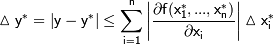
Partial derivatives (D in degrees):
a) for d: f(d) = d/21*2*arctg(5.25/16.7) = 1.662061807*d. The partial derivative is 1.662061807 and the part of absolute error 1.662061807*0.08 = 0.1329649446 (degrees).
b) for f: f(f) = 12.8/21*2*arctg(5.25/f) = 1.219047619*arctg(5.25/f). The partial derivative in radians is -20479954636/(3199992912*f^2+88199804637) (computed with http://www.numberempire.com/). Substituting f = 16.7 gives us -0.0208842 (the absolute value is 0.0208842) and the absolute error = 0.0208842*0.3 = 6.26526e-3. In degrees this is 0.3589729556.
Total error is 0.1329649446+0.3589729556 = 0.4919379 (degrees) = 0 deg. 29 min. 30.98 sec.
The real value of D computed by Carnicom is 21 deg. 16 min. +- 0 deg. 29 min. 30.98 sec. The precomputed value of 21 deg. 37 min. 37.77 sec is within the error margin.
I'm interested if some errors exist in my computations.
Last edited by a moderator:


