Calculating the height of something in a P900 photo when distance is known

[Mick West]

Update May 2 2017

The following discussion has a error in that it was assumed the field of view was the same at long distances as it was at 8m. In fact the field of view narrows with longer focus. This alters the scale factor from 0.02 to 0.01737 for a P900 at full zoom and focussed on something over 100 meters away. Discussed at: https://www.metabunk.org/posts/205386/

Hence the sizes calculated below should be reduced by 15%. This does not significantly alter any of the conclusions

There have been some discussions on using photographs to calculate the distance to something if the height is known. The math is relatively simple once you've got the correct figures for your camera. Here I'm going to look at a specific case with the P900 camera (popular among Flat Earthers and Chemtrail enthusiasts) and show how to get the relevant numbers and then use them.

Here I'm assuming we;d be using full zoom of 2000mm, and no digital zoom. Different zoom settings will be discussed.

Essentially what we want to find the the field of view, i.e. the angle between the left side of the image and the right side. The more we zoom in, the narrower the field of view becomes.

A more straightforward way of expressing the field of views is as a ratio between the width and the distance. In the above image I've set a rule at 8m (8000mm) from the camera, and we can see the width of the image covers about 160mm, so the FOV ratio is 160/8000 or 0.02 (within the bounds of measurement error)

This means that the width covered by the photo at a distance D is D*0.02. We can easily verify this for the image above. It's a 8m, so 8*0.02 = 0.16m = 160mm

Since FOV is just an angle, the FOV ratio remains the same regardless of distance. So if the image is 160mm wide at 8m then it will be 1600mm (1.6m) wide at 80m, and 1.6km wide at 80km.

So to find the length of anything in a 2000mm focal length P900 image at distance D, then we just need to scale it relative to the image width, so it's the D*0.02*(Object Length)/(Image Width)

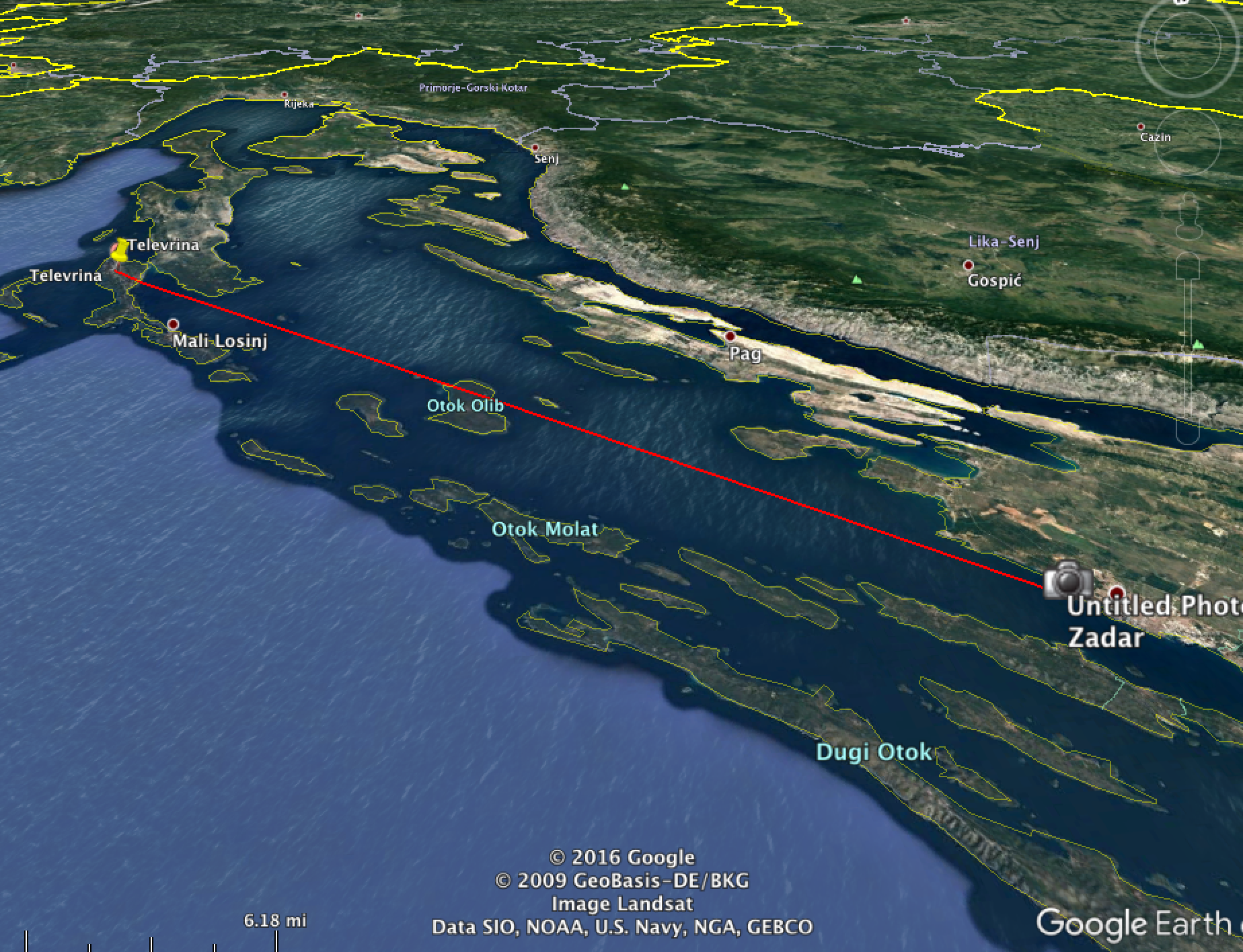
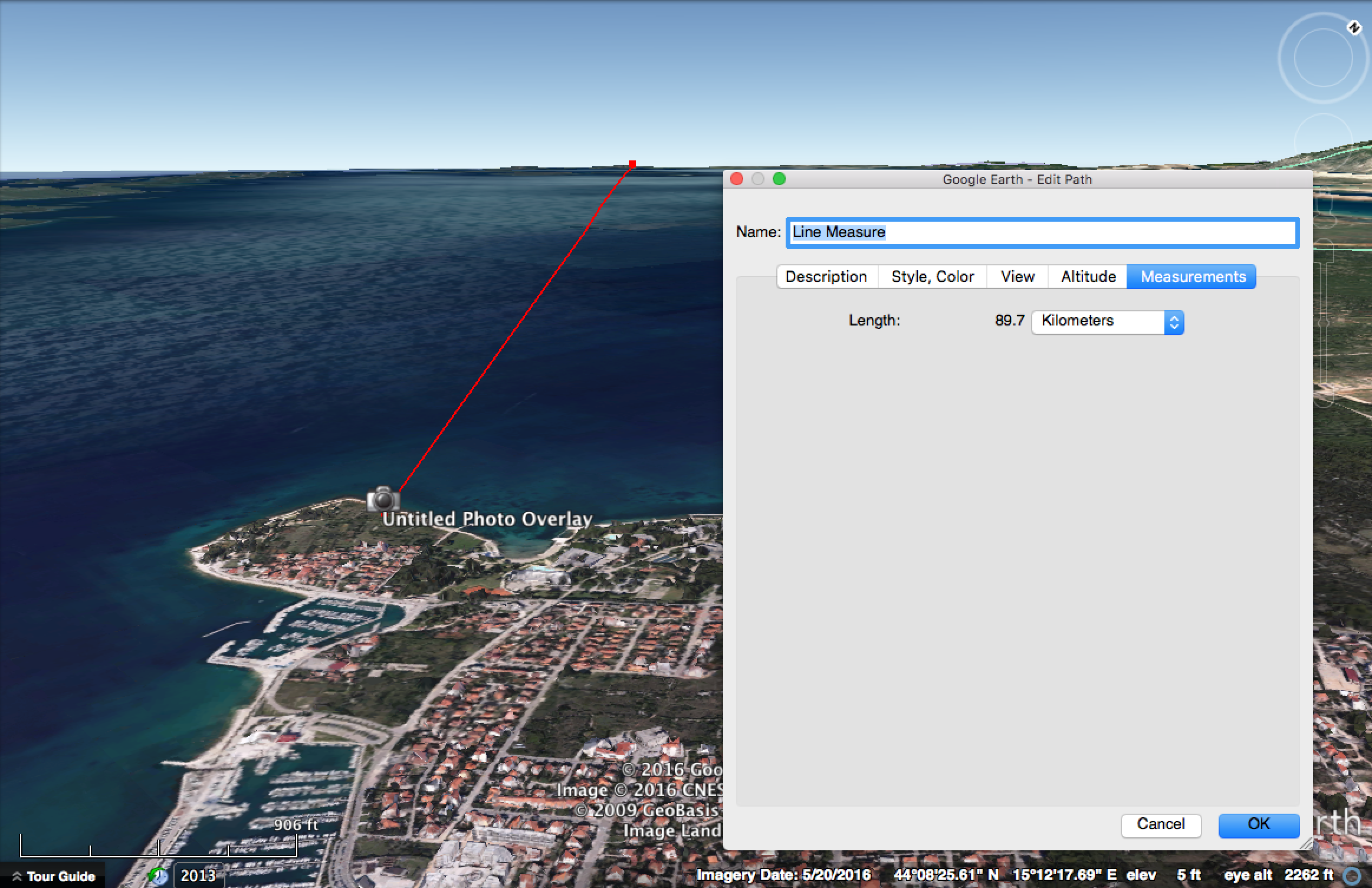
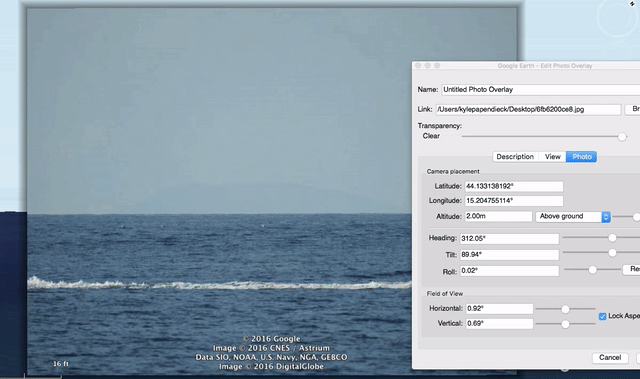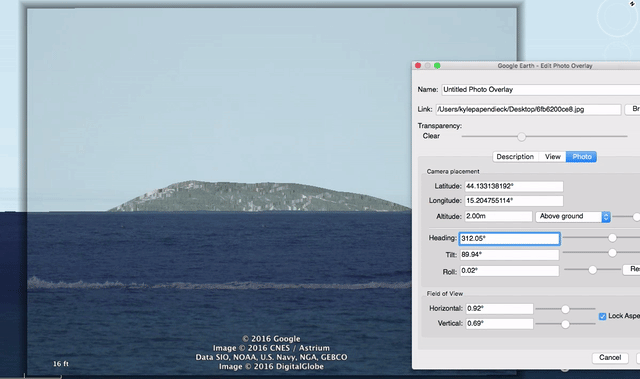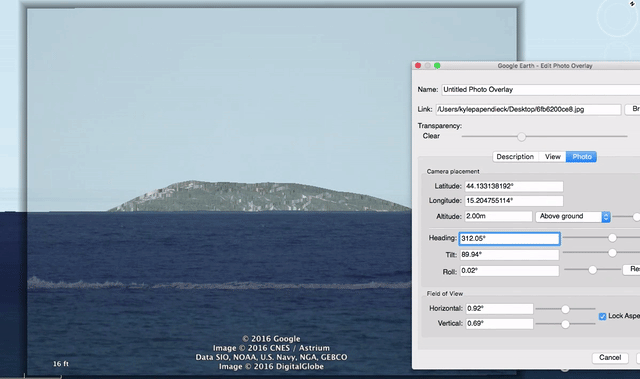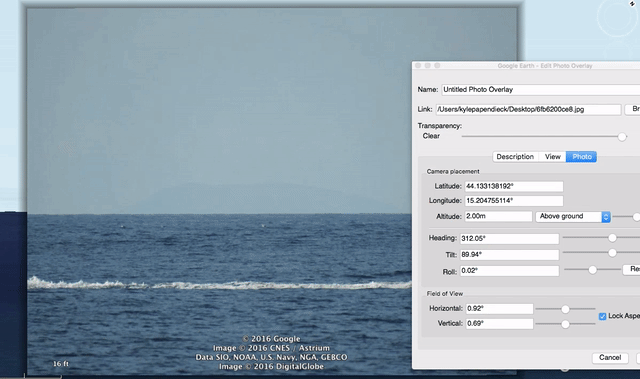
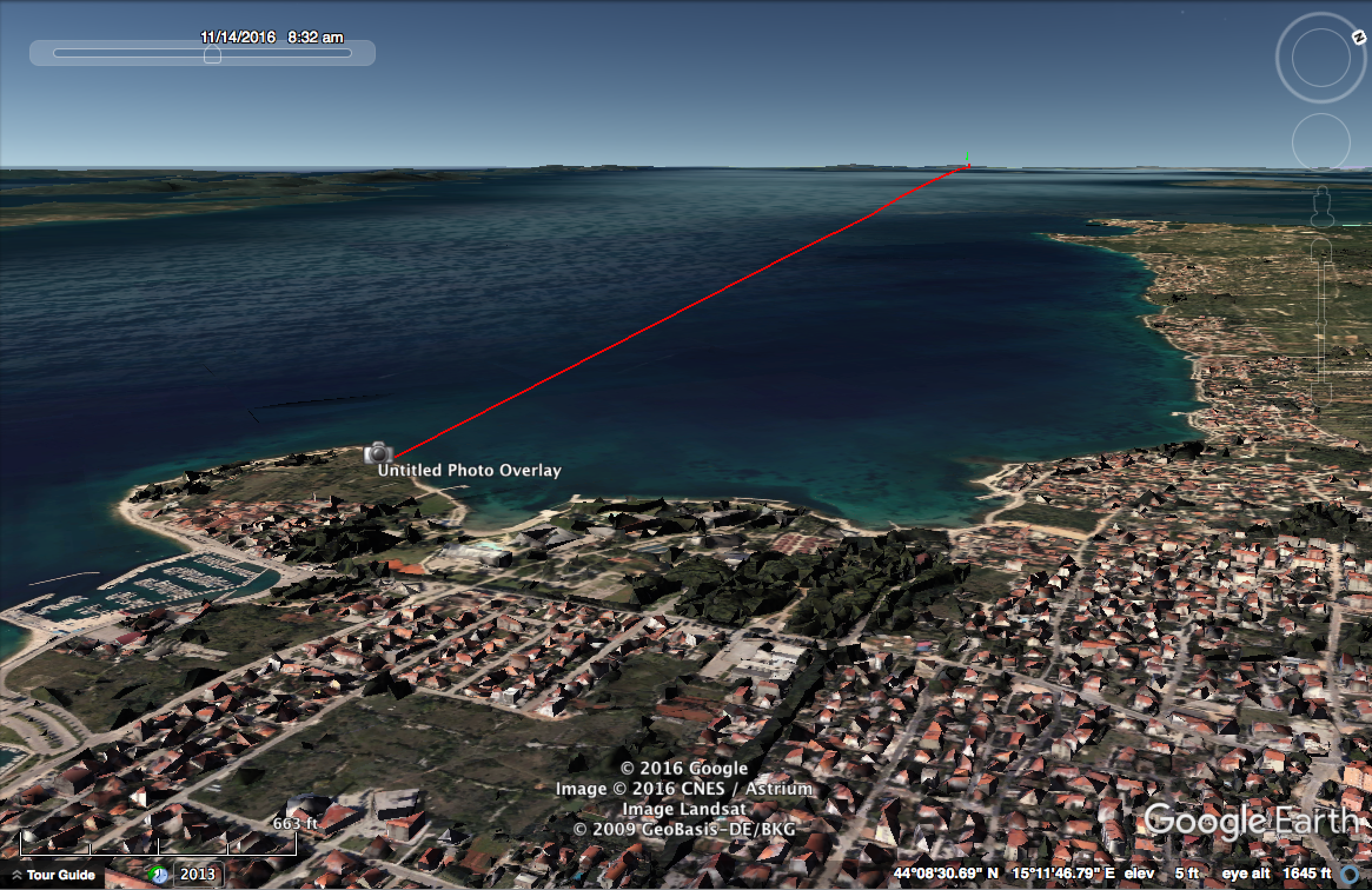
So, a practical example, here's a P900 photo of an island. (Posted in the comment of an accompanying video that shows the approximate viewpoint)

The photo is taken from Zadar in Croatia. The Island is Losinji, The mountain is Televrina, the high point of which is 589m above sea level and 91.8 km from the view point.

What we are interested in here is how much of the mountain is visible above the horizon. Now in this shrunk version of the image, the width is 1440 pixels, D (distance) is 91800m, so for an object of length L pixels in this image, the actual size 91.8km away is 91800*0.02*L/1440

The visible height is 90 pixels:

So 91800*0.02*90/1440 = 114.75, or about 115m.

So of the 589m of the mountain that would be visible from a higher viewpoint (or on a theoretical flat Earth) only 115m is visible, so 474m of the mountain is hidden by the horizon. That's about 80% hidden

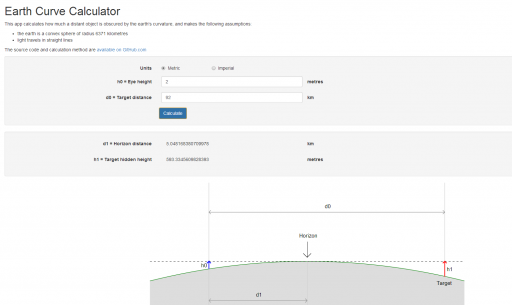
We can verify this is a sensible figure in two ways, firstly with a horizon calculator. We also need to know the height of the camera, I'm assuming they are standing on the top of the steps (2m) with camera at eye level, so around 3.5m
https://www.metabunk.org/curve/?d=91.8&h=3.5&r=6371&u=m&a=n&fd=60&fp=3264

Distance = 91.8 km (91800 m), View Height = 3.5 meters Radius = 6371 km (6371000 m)
Horizon = 6.68 km (6678.1 m)
Bulge = 165.35 meters
Drop = 661.41 meters
Hidden= 568.62 meters

With Standard Refraction 7/6*r, radius = 7432.83 km (7432833.33 m)
Refracted Horizon = 7.21 km (7213.17 m)
Refracted Drop= 566.91 meters
Refracted Hidden= 481.29 meters

A pure geometry calculation gives a hidden value of 568m, but when we account for standard refraction in the atmosphere, then the hidden value is 481m, close to the measured 474m

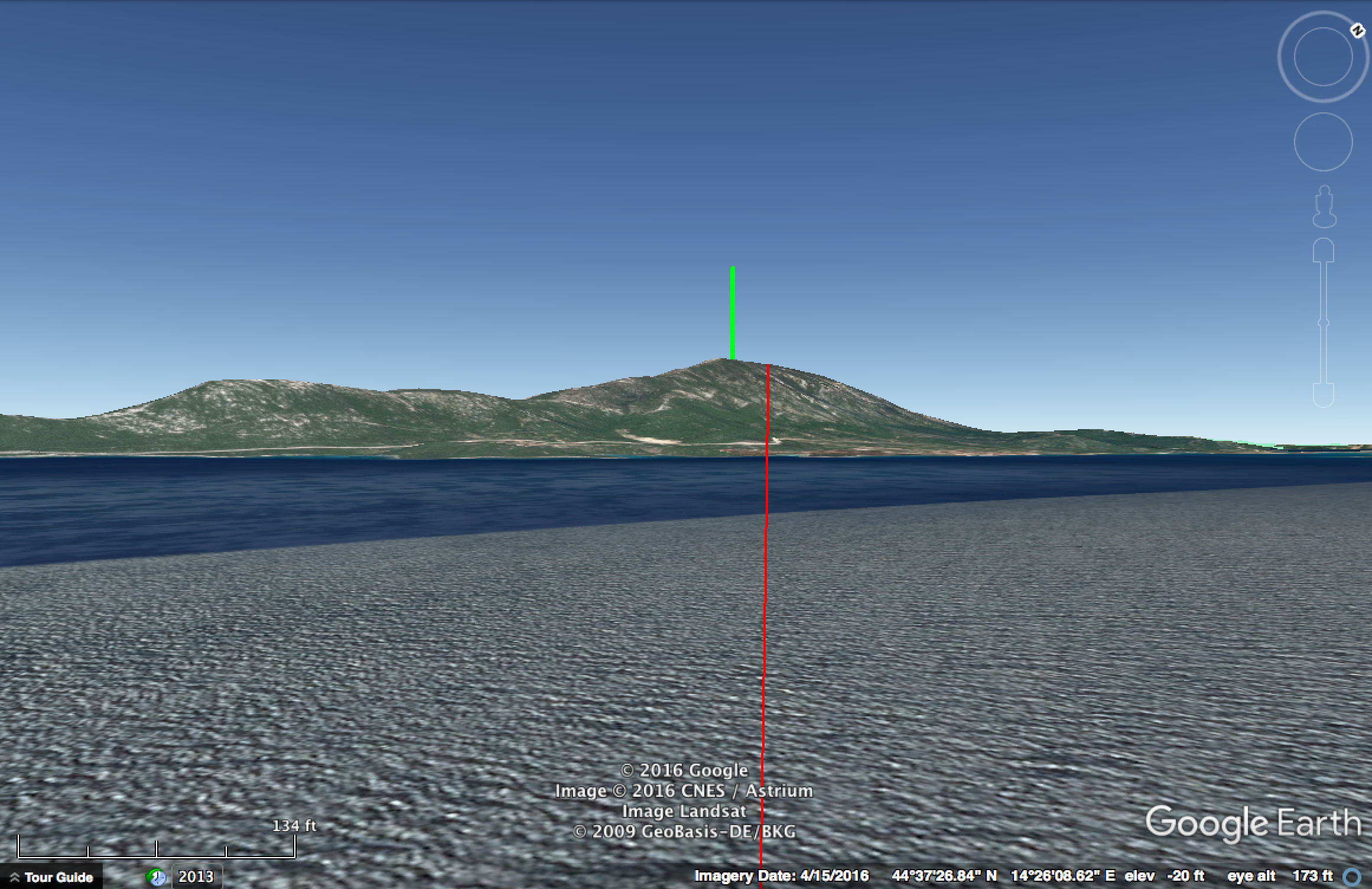
Then we can also compare what we see against a view of the island for the same distance, but a few hundred meters in the air (so we can see the full height), then over the photo, and mark the horizon in the photo vs the actual horizon.

Now this is somewhat rough due to the 3D nature, but the result is 157/224, or 70% hidden, the camera calculation showed 80% hidden, but well within the correct ballpark, and all certanly enough to demonstrate the curvature of the ocean surface.


Addendum. The above is a little hard to follow, so here's maybe an easier way of looking at it.

Here's an example of something of known height and distance. The Cooling tower of The Rancho Seco Nuclear Generating Station, viewed from Holly's Hill Vineyard.

601 pixels high, image width is 4608
52 km away

so 52000 * 0.02 * 601 / 4608 = 136m, 446 feet

Internet says the towers are 426 feet high. Looks like I slightly over-measured, but certainly in the right ballpark.

 

[Abishua]

I am the flatearther d

Good work Mick, I'm the "planer" guy that took the picture from Zadar.

I just have one question.. how do you explain away this kink that indicates your math is wrong?
There is no "kink" in the google upper rendering of the island that you claim we are seeing on the picture.. but there is a distinct kink in the middle of google rendering of the entire island.. and we can clearly see that kink in both pictures I took of the island.. as well as we can clearly see the less steep descending angle of the island that follows after the kink.. that angle is not present in the top part of the island only.. and those things indicate that almost entire island is visible and you made a mistake somewhere in your calculations..

 

[deirdre]

how do you explain away this kink

pixel weirdness from trying to enhance a washed out pic.

That's why your mountain shape doesn't match the mountain shape at all. The top pic in your display is alot pointier. The distance from your "kink" to the top of the mountain (top pic) is as long as the apex of the mountain. But this is not so in the lower pic. and where is the "kink" (#2) in your lower pic?

when i enhanced the pic it looks different from yours.
the little top blob in the original pic is partly missing on your enhanced pic. (pixel issues)

 

[Ray Von Geezer]

I am the flatearther d

Good work Mick, I'm the "planer" guy that took the picture from Zadar.

I just have one question.. how do you explain away this kink that indicates your math is wrong?
There is no "kink" in the google upper rendering of the island that you claim we are seeing on the picture.. but there is a distinct kink in the middle of google rendering of the entire island.. and we can clearly see that kink in both pictures I took of the island.. as well as we can clearly see the less steap descending angle of the island that follows after the kink.. that angle is not present in the top part of the island only.. and those things indicate that almost entire island is visible and you made a mistake somewhere in your calculations..

I don't think you're taking into account that you're comparing a zoomed image of the top of the mountain with a subset of a full picture. You've placed your arrows as if the two were scaled the same horizontally, they aren't as can be seen by comparing the undulations on the top. Consequently what you think is the same "kink" can't be.

Here's some MSPaint hamfistedness to demonstrate a closer comparison:-

Ray Von

 

[Mick West]

Another verification of the visible height is the radio tower visible on the photo

It's very roughly a third of the height of the visible portion of the island. Given the photo calculation of 115m this would make it around 38m

If however the photo was depicting the entire island (which it is not, as explained above) then that that would make it 196m high.

There's a fence around the antenna that is probably shorter than that van, but let's say 2m to be conservative
[Broken External Image]:http://l7.alamy.com/zooms/da11a5a47...enna-located-on-osorscica-mount-on-bxp0jy.jpg

The microwave dish's are about 1/12th the height of the tower, so around 3m in diameter. Roughly consistent with reality. (Probably more like 4m, with perspective)

(second photo is of a similar tower with typical microwave dishes)

If the tower were actually 196m high (which it's not), then the dishes would be 16m in diameter, which is clearly impossible.

So, all the facts point show that we are just seeing the top portion of the island in these images, and hence the curve of the ocean obscures the rest.

 

[Mick West]

I forgot to link to the video in the OP, I've added a link now, and here:

Source: https://www.youtube.com/watch?v=WV8DmbOS5Ts

 

[Mick West]

as well as we can clearly see the less steep descending angle of the island that follows after the kink.. that angle is not present in the top part of the island only..

This is actually a valid observation, and is typical of this type of image. The reason being that the closer you get to the horizon the more compressed the image is from the effects of refraction. This has the effect of making the slope less steep closer to the horizon.

 

[Mick West]

I've verfied that the "kink" is actually a video artifact. I dowloaded the videof rom YouTube, and used a "Levels" filter in Adobe Premier. at 00:53:08 you see there's no kink (although there is the reduction in slope from refraction, as described above)

Then at 00:54:50 there's glitch as the image stabilization resets:

Here's two consecutive frame, showing the glitch happening.

If you look at the entire video in enhanced contrast you can see the contour waves around quite a bit during these movements. But there are portions when it is stable, and then it matches the photo.

Another interesting thing is that the radio tower is actually visible in the video, just rather flickery.

 

[Mick West]

On a more general note, I think that mountains disappearing over the horizon is a much better falsification of the Flat Earth theory than boats. While the boats example is still valid, it's quite hard to observe and the effects of refraction make it confusing to interpret. It's also hard to repeat as you need a good boat.

Mountains, on the other hand, rise up above the distorting effects of refraction and you can usually get a very good fit to the peaks using Google Earth which allows you to show exactly how much is obscured by the horizon.

They are also very repeatable, weather permitting the distant mountain is generally visible in the same way many days of the year. For example observing the partial hiding of Catalina Island is an easy experiment anyone in Los Angeles can do with a quick ride to the beach.

I think perhaps I'll start a thread collecting these examples, with locations, so that people can replicate them if they are having doubts about the rotundity of Earth.

 

[Abishua]

This is actually a valid observation, and is typical of this type of image. The reason being that the closer you get to the horizon the more compressed the image is from the effects of refraction. This has the effect of making the slope less steep closer to the horizon.

Why is that distortion not present on the right then? You claim half of the island is distorted but you can make out the tower on it? Well funny how its "distorted" in a way to match the island shape and angles.. I appreciate your effort.. but untill you have something better as evidence I am going to beleive my own eyes..

and even if that was the top of the island you forget you still have few major problems..

1. bottom of the island could still be hidden by a mirrage effect enhanced over great distance and not a "curve", so can you be intelectually honest and objectivly research is it the mirrage that is doing the hiding or is it the curve?

2. since I am the one who took the picture and I know how close the waves reached the top of the peer.. and the image was taken from shortened tripod.. saying it was 1.5 meter above the sea level would be too much as observer height.. but let me be generous towards you and say it was 2m.. observer height.. at those numbers even the very top of the island should be hidden far bellow the curve..

3. and even if that top was above the curve.. lets be generous again and say 100m above the curve.. how would those 100m of landmass height penetrate the mirrage effect at 92km away, when Olib can not do it at 42km away? You see.. it's riddled with serious issues..

on the other hand it all makes perfect sense on a flat earth.. mirrage is hiding some of the bottom.. top is visible because it is out of that distortions reach.. vuola

 

[Ray Von Geezer]

Why is that distortion not present on the right then? You claim half of the island is distorted but you can make out the tower on it? Well funny how its "distorted" in a way to match the island shape and angles.. I appreciate your effort.. but untill you have something better as evidence I am going to beleive my own eyes.

But your picture doesn't match the mountain, at all, and it's immediately obvious. That's what was curious about the comparison you made with the "kink" glitch - it was the only thing that did match, other than that they could be the silhouettes of any two bits of scenery. Your picture couldn't even really be described as portraying a mountain.

On the other hand your picture is a very close match for the top of the mountain alone, and the very part Mick's calculation says your picture is actually showing. Don't you think that's quite a coincidence?

Ray Von

 

[Spectrar Ghost]

3. and even if that top was above the curve.. lets be generous again and say 100m above the curve.. how would those 100m of landmass height penetrate the mirrage effect at 92km away, when Olib can not do it at 42km away? You see.. it's riddled with serious issues..

Olib has a height of 74m, just a little more than 1/8 the maximum height of Losinj. The refracted hidden height at 1.5m height and 42km distance is about 93.5m.

 

[Abishua]

Olib has a height of 74m, just a little more than 1/8 the maximum height of Losinj. The refracted hidden height at 1.5m height and 42km distance is about 93.5m.

View attachment 22582

there is no curve here.. only mirrage.. I claim the same for Olib.. only at a greater distance..

 

[Abishua]

But your picture doesn't match the mountain, at all, and it's immediately obvious. That's what was curious about the comparison you made with the "kink" glitch - it was the only thing that did match, other than that they could be the silhouettes of any two bits of scenery. Your picture couldn't even really be described as portraying a mountain.

On the other hand your picture is a very close match for the top of the mountain alone, and the very part Mick's calculation says your picture is actually showing. Don't you think that's quite a coincidence?

Ray Von

actually to explain the ball version of events you need much more coincidence and imagination.. and it simply does not match with what we see..

even the top of the island should not be visible... and even ff there was 100m of land visible at that distance of 92km that 100m would be obscured and completeley "deleted" by mirrage.. just like Olib is.. and this road is.. so earth is flat.. sorry guys..

 

[Abishua]

could you guys at least accept the possibility of earth beeing flat? and thats why these things happen?

 

[Ray Von Geezer]

actually to explain the ball version of events you need much more coincidence and imagination.. and it simply does not match with what we see..

even the top of the island should not be visible... and if even ef there was 100m of land visible at that distance it would be obscured and "deleted" by mirrage.. just like Olib is.. and this road is.. so earth is flat.. sorry guys..

Personally, I don't want to get tied up in the old flat vs ball earth thing, I'd much rather stick with reality.

That reality is that your picture matches just the top of the mountain very closely, and it matches the whole mountain hardly at all. There's no imagination required to come to that conclusion, so whether you can incorporate it into your world view or not is up to you

Ray Von

 

[Abishua]

Personally, I don't want to get tied up in the old flat vs ball earth thing, I'd much rather stick with reality.

That reality is that your picture matches just the top of the mountain very closely, and it matches the whole mountain hardly at all. There's no imagination required to come to that conclusion, so

Ray Von

The reality is that top of the mountain should not be visible at al.. and whether you can incorporate it into your world view or not is up to you.. you can also keep making excuses to continue your beleif in a worldview that is flawed.. and that my friend.. is not called sticking with reality..

 

[Ray Von Geezer]

The reality is that top of the mountain should not be visible at al.. and whether you can incorporate it into your world view or not is up to you.. you can also keep making excuses to continue your beleif in a worldview that is flawed.. and that my friend.. is not called sticking with reality..

See you say that, yet at the top of this thread is a calculation that predicts what should be visible from the viewpoint where you took your video and pictures. When the images you took are compared to that prediction, they match.

Conversely, what you claim your images show (the whole mountain) doesn't match.

Again, that's not flat vs ball earth, the conflict here is between the reality of your images matching the top of the mountain, and your belief that your picture shows the whole mountain. Clearly the evidence shows your belief, in this instance at least, is wrong.

Ray Von

 

[Abishua]

See you say that, yet at the top of this thread is a calculation that predicts what should be visible from the viewpoint where you took your video and pictures. When the images you took are compared to that prediction, they match.

Conversely, what you claim your images show (the whole mountain) doesn't match.

Again, that's not flat vs ball earth, the conflict here is between the reality of your images matching the top of the mountain, and your belief that your picture shows the whole mountain. Clearly the evidence shows your belief, in this instance at least, is wrong.

Ray Von

Not true.. I entertained the possibility that what we are seeing truly is only the top of the mountain.. even though certain features of the island and photo of it make that at least very doubtfull.. my point simply is.. even if that is only the top.. it still does not work on your theoretical model of earth.. it still should not be visible.. lets say mirrage is hiding bottom part of the island.. then top is visible.. no problem there.. but if there was a curvature of earth.. and that bottom was obscured by curvature (even though when we do the math everything should be obscured by curvature) then the hypothetical remaining visible 100m that would hpothetically be aboove the hidden curve could never "escape the mirrage".. so mirrage would completley delete the rest of that small protruding part of land..

so I m simply using logical thinking to show you how flawed this theory truly is.. I want us to do real science.. not scientism... the difference between science and scientism, is that science takes data and adjusts the theory to match data.. and scientism takes theory and adjust the data to match the theory.. so scientism is a dangerous religion that can destroy a persons pursuit of truth.. or what factual data and evidence show..

I don t want us to be religious.. I am open to any outcome of this.. but only by following real mesurable logical data.. if we start making shit up to match with what the theory is.. we are doing a diservice to truth.. and to eachother..

 

[Mick West]

1. bottom of the island could still be hidden by a mirrage effect enhanced over great distance and not a "curve", so can you be intelectually honest and objectivly research is it the mirrage that is doing the hiding or is it the curve?

Yes, the refractive index of air would not hide that much, and certainly not consistently. Normal atmospheric refraction actually makes MORE of the island visible, not less. That island is visible from that spot all the time.

And there are countless other similar examples of large islands being consistently hidden by the horizon.

Not true.. I entertained the possibility that what we are seeing truly is only the top of the mountain.. even though certain features of the island and photo of it make that at least very doubtfull.. my point simply is.. even if that is only the top.. it still does not work on your theoretical model of earth.. it still should not be visible.. lets say mirrage is hiding bottom part of the island.. then top is visible.. no problem there.. but if there was a curvature of earth.. and that bottom was obscured by curvature (even though when we do the math everything should be obscured by curvature) then the hypothetical remaining visible 100m that would hpothetically be aboove the hidden curve could never "escape the mirrage".. so mirrage would completley delete the rest of that small protruding part of land..

What mirage? Your argument makes no sense. You are invoking a special super-mirage to explain why on a hypothetical flat Earth the bottom 2/3 of the mountain would be hidden, and then saying this proves the earth is flat because the mirage would hide all of the remaining mountain on a round Earth.

Your images match exactly what would be expected on a round earth with standard refraction. You don't need to invent some incredible impossible mirage to explain them. The Earth is simply round, and that explains everything.

 

[Spectrar Ghost]

A pure geometry calculation gives a hidden value of 568m, but when we account for standard refraction in the atmosphere, then the hidden value is 481m, close to the measured 474m

So we can all see what we're discussing.

Without taking refraction into account, the mountain would indeed be over the horizon. However, standard refraction makes more of the island visible, not less. This is because air becomes less dense with altitude, and refraction always bends light towards higher density (strictly speaking, higher index of refraction, but the two are equivalent for our purposes). Thus even on a flat earth your "hidden by mirage" theory directly contradicts simple optics.

Do you really think it's more likely that the earth is flat and there is a persistent, consistent mirage everywhere that breaks the laws of optics, than that the earth appears round because it actually is?

 

[Mick West]

Without taking refraction into account, the mountain would indeed be over the horizon.

Not entirely, 568m hidden out of 589

 

[Spectrar Ghost]

At 3.5m. Given the assertion that the height was closer to 2m, it's safe to assume the entire mountain would be below the true horizon.

Changes nothing about the conclusion though.

 

[Bruno D.]

could you guys at least accept the possibility of earth beeing flat? and thats why these things happen?

There are ZERO evidences for a flat earth, so no, I couldn't.

I accept the possibility of Aliens among us, Lizard People or a Matrix more than accept the idea of a Flat Earth, simply because in these three examples, there are no evidences for or against it, while for a flat earth there is a huge amount of evidence against it.

 

[Abishua]

Ok.. so you guys beleive that atmospheric mirroring with greater distance makes things more visible, and I beleive it makes things less visible.. the larger the surface area is that creates the "mirror" the more hidden things are behind it..

My conclusion after all this is that mirrage blocked some of the bottom view of the island.. and the rest is visible not because of magical refraction.. but because earth is flat..

just like this video proves earth is flat..
Source: https://youtu.be/DPDtMQqlprk

[... off topic material removed]

 

[Mick West]

Ok.. so you guys beleive that atmospheric mirroring with greater distance makes things more visible, and I beleive it makes things less visible.. the larger the surface area is that creates the "mirror" the more hidden things are behind it..

Perhaps you could draw a diagram from the side showing how that would work?

Consider what you are looking at here:

Here's what you are claiming is caused by "refraction" or "mirroring"

In particular how is this perfect undistorted perspective correct image of the ocean surface with seagulls on it somehow a "mirror"

And in a wider context

Look at the boats near the horizon. The island would be behind them. How does that work with "mirroring"?

It just makes no sense with a flat earth. And yet is EXACTLY what you would expect on a round Earth.

 

[Ray Von Geezer]

My conclusion after all this is that mirrage blocked some of the bottom view of the island.. and the rest is visible not because of magical refraction.. but because earth is flat.

Yet yesterday you believed your images showed the whole mountain. Even thought they looked nothing alike.

Would you call making the evidence fit your belief rather than the other way around science, "scientism", or something else?

Ray Von

 

[Abishua]

I am still not convinced it is not the whole mountain.. I mean.. just look at it.. look at that kink.. just look at it.. and its present on both different images I took.. and to the right that slope is just like bottom slope on the island..

 

[deirdre]

I am still not convinced it is not the whole mountain

Mick already showed you from the very video you are using, that that kink is just a artefact of the camera trying to adjsut.

Your kink doesnt even line up. It's not the whole mountain. (and how do you explain the size of the antenna?_

 

[Rory]

Mick's "size of the antenna" calculations clearly show that nowhere near the whole of the mountain is visible above the horizon.

Forgetting about the round/flat earth questions, it's clear to see that only the top 20% or so of the mountain is visible.

Can agree on that? Surely the only reason to dispute that is to try and to make the photo fit a preconceived theory.

Also, the video linked to by @Abishua a few posts above is explored, explained and debunked here:

https://www.metabunk.org/debunked-view-of-blue-ridge-mountains-impossible-on-spherical-earth.t7941/

 

[Mick West]

Mick's "size of the antenna" calculations clearly show that nowhere near the whole of the mountain is visible above the horizon.

As do the P900 image size calculations, and the shape of the top of the mountain.

And it's not like this is the only mountain in the world that's a few tens of kilometers off the coast. There's thousands of such mountains and they all do this. They all look like they are being obscured by the curvature of the earth.

 

[Bass In Your Face]

It seems to work out fine in Google Earth. I just picked a spot on the shore of Zadar, trying to get the photo to fit *exactly* is hard if it isn't the right location but its close enough.

This is what the mountain looks like when you get alot closer:

Red line = the straight line from the photo marker to the mountain marker
Green tower = where the tower is located on this island

Maybe Abishua can point out his exact location in this photo:

 

[Mick West]

It seems to work out fine in Google Earth. I just picked a spot on the shore of Zadar, trying to get the photo to fit *exactly* is hard if it isn't the right location but its close enough.

I forgot I only posted my GE reconstruction on Facebook, attached.

The location appears to be the Sea Organ (2km south of your spot), the video is from the path up the steps behind here:
https://www.google.com/maps/place/Z...13f40784!8m2!3d44.119371!4d15.2313648!6m1!1e1

The photo is described as being on the pier, presumably level with the top of the sea organ at 2m.

 

[Abishua]

Mick, I was just wondering using the same math you used up there, how large do you get these moon craters are? Lets say tycho.. wiki says its 86km..

Here is one image I took of the moon..
http://www.megafileupload.com/kxgG/DSCN0350.JPG

 

[Mick West]

Mick, I was just wondering using the same math you used up there, how large do you get these moon craters are? Lets say tycho.. wiki says its 86km..

Sure, but you need to know how far away the moon is in order to do that. Let's use my photo of the Supermoon, as we know the distance, about 356500 km

Tycho is about 64 pixels wide, and the image is 4608

356500*0.02*64/4608 = 99 km

Remember this is an approximation, it just gives you a ballpark figure. But it's about in keeping with measuring the same line on Google Moon:

 

[Abishua]

Ok.. thanks.. I get 101.5km out of those numbers.. so 15% error.. thats not so bad.. it's just strange to me we can see something about 90km large at 356 000km away with our bare eyes.. Not sure how perspective math on that works.. but let's say earth was flat and there was no atmosphere at all, and I was looking at NY from lets say spain.. would I see manhattan? and this is just few thousand kilometers away... we are talking 356 000km here..

 

[Mick West]

Ok.. thanks.. it's just strange to me we can see something about 90km large at 356 000km away with our bare eyes..

Tycho is not exactly visible in any detail to the naked eye though.

It's the same as seeing something that's 90mm from 356000mm (356m) away.

Not sure how perspective math on that works.. but let's say earth was flat and there was no atmosphere at all, and I was looking at NY from lets say spain.. would I see manhattan? and this is just few thousand kilometers away... we are talking 356 000km here..

The math is just: Visual Size = Actual Size / Distance

You would technically see NY yes, but it would be like a short jaggy line on the horizon, as it's not incredibly tall compared to it's length. Here's 10km worth

 

[Abishua]

Tycho is not exactly visible in any detail to the naked eye though.

It's the same as seeing something that's 90mm from 356000mm (356m) away.



The math is just: Visual Size = Actual Size / Distance

You would technically see NY yes, but it would be like a short jaggy line on the horizon, as it's not incredibly tall compared to it's length. Here's 10km worth
View attachment 22760

Yeah.. well too bad we have to have the distance before we can calculate the size.. because we can put 3565km as distance, and get that tycho is 1km in size.. is there a way we can somehow get results that we can actually check and test for ourselves? Without using external sources that we cannot verify on our own?

 

[Mick West]

Yeah.. well too bad we have to have the distance before we can calculate the size.. because we can put 3565km as distance, and get that tycho is 1km in size.. is there a way we can somehow get results that we can actually check and test for ourselves? Without using external sources that we cannot verify on our own?

The simplest way in terms of math is the parallax method, where you see the change in position of the moon relative to the starfield (which is essentially fixed when viewed from Earth). However it required two people a long distance (like 1000 miles) apart to take simultaneous photos of the moon when it is fairly close to a bright star.
https://www.khanacademy.org/partner...e/measure-the-solarsystem/a/parallax-distance

There are several other methods, but they generally require you to know the radius of the Earth. The parallax method only requires that you know the distance between the two people. Synchronizing the photos should be straightforward enough with cell phones.

 

[Abishua]

Here is where I have a problem.. http://www.dailymail.co.uk/sciencet...hanks-study-puts-distance-just-1-6-miles.html

This article states that a candle after 2.5km or 1.6 miles is not visible anymore to unaided human eye.. lets say the candle flame is 2.5cm high.. so this is a ratio of distance to size in km 2,5 : 0.000025 or.. 100 000:1

soo at 100 000km away we should see a candle 1km tall.. so at supposed moon distance we should see a candle that is 3.5km high.. no problem there.. I guess if it was surrounded by blackness of space it is possible we could see it at that distance..

now.. here comes the problem.. as they say closest star is about 4.23 lightyears away from us.. a light year is 9.46 x 10 to 12th power.. so that is 40015800000000 whatever that number is km away from us.. so.. does this mean that the star in question is 400158000km large?