Interesting things happen when you put refraction into the flat earth model. Here's standard refraction from 10 feet.
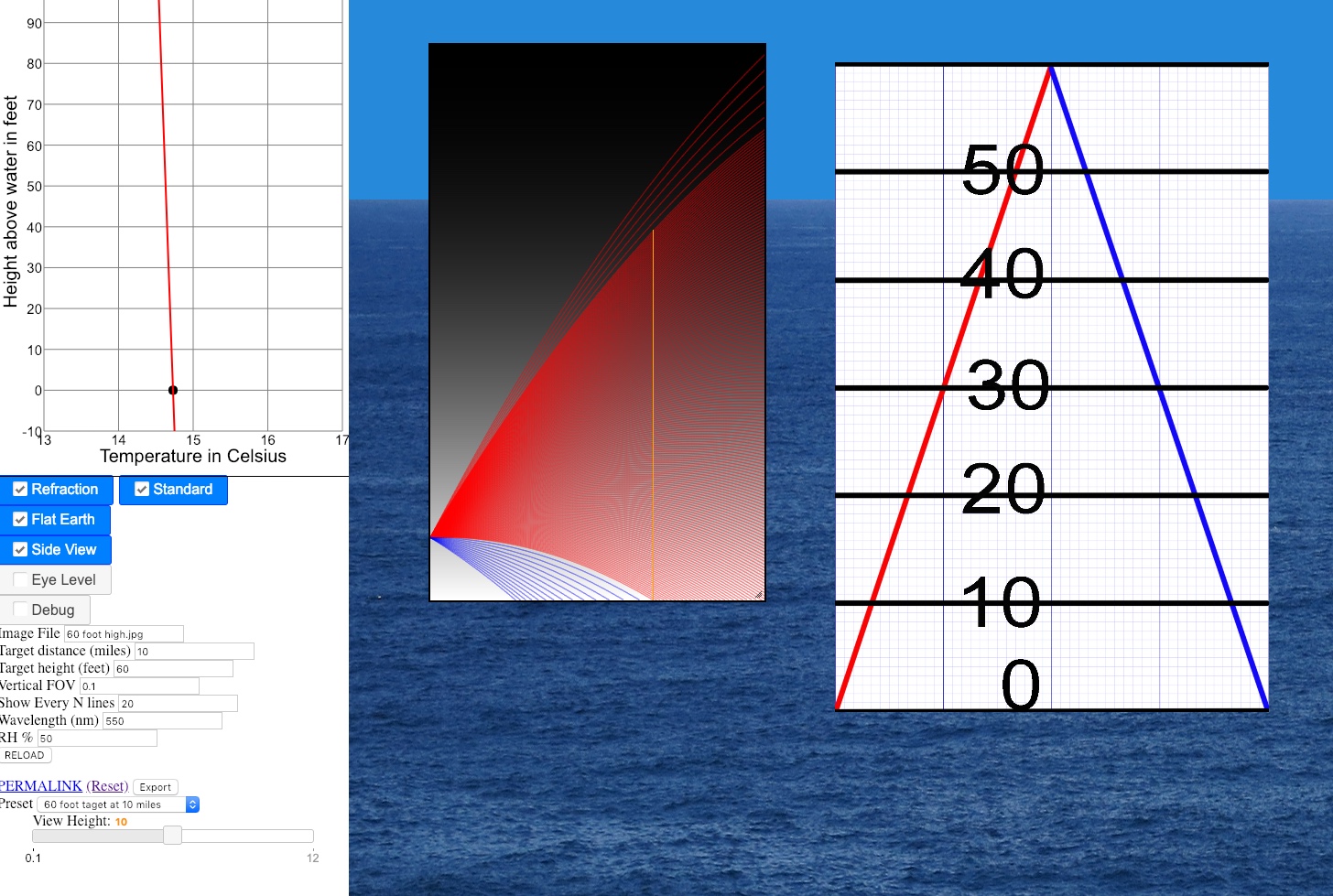
Look where the horizon is! The standard atmosphere is denser lower down due to air pressure, so all rays bend down, and over a long distance they hit the water. This raises up the horizon in the image quite a bit.
It's not at all as dramatic as it looks though, the vertical field of view here is 0.1° (vs. about 0.75 for a P900)
Look where the horizon is! The standard atmosphere is denser lower down due to air pressure, so all rays bend down, and over a long distance they hit the water. This raises up the horizon in the image quite a bit.
It's not at all as dramatic as it looks though, the vertical field of view here is 0.1° (vs. about 0.75 for a P900)
