Hello! I wanted to reply here in regards to Nick Hovak's new video he put up a couple days ago. In that video, he makes the claim that he can see 8,000 feet of Pikes Peak.
Source: https://www.youtube.com/watch?v=09TwUYK1XLg
I want to focus on the image we see in his video at
10:43. This is the point in the video that I found that had the clearest image of the mountain on the features to the right of it. I edited the screenshot some to get a clearer, sharper image of the mountain's features against the haze and sky. I came up with this image.

What I wanted to do was find out where Sentinel Point is in this video because that will help us later on. I found used Google Maps to get the exact coordinates where he zoomed in to get the above image. This gave me 40.754369, -104.993504.
To find Pikes Peak, I put these coordinates into Peak Finder. I zoomed in as far as I could and looked directly south and got this image:
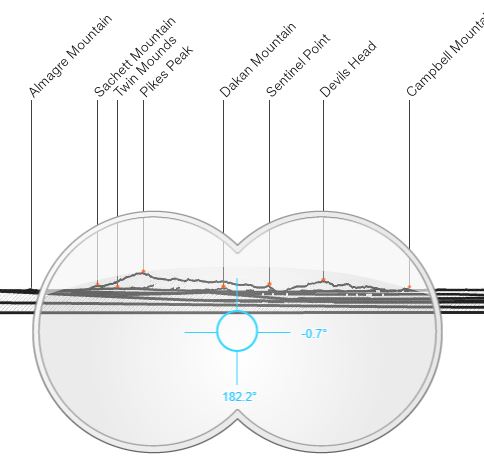
I'll use this later. Let's go back to the first image.
We can use Nick's estimate of 8,000 feet as a marker. If Nick suggests that we can see 8,000 feet of the mountain, then this can be used as a gauge to determine how far away these sharp points are in the image. From that image, I came up with this one. So, I used MS Paint to draw a line from the top of the obstruction in front of Pikes Peak to the top. This became my scale to determine 8,000 feet. I dragged this line off to the side and locked its dimensions. From Pikes Peak, I drew a vertical line (used a photo editor with a snap-grid to ensure it was perfectly vertical within the program). I did this for the first sharp peak to the right of Pikes Peak as well. I then used the 8,000 foot line I created and copied it to my clipboard (setting the copy to transparent). With this, I copy/pasted multiples of these line segments in increments to the right, using the snap grid to ensure I stopped one where the other one ended (I also raise/lowered it a bit for clarity to visually see where each 8,000 foot marker stopped/started).
What this gave me is a line that I can use to measure the ground distance between Pikes Peak and the first sharp peak to the right of Pikes Peak. From this, it was about 2.4 line segments. Using each of these lines as a gauge for 8,000 feet, I multiplied 8,000 by 2.4 to get 19,200 feet. I know these are VERY crude estimates, but bear with me. If 8,000 feet of Pikes Peak is visible in this video and the screenshot I included above, then the first sharp peak is about 19,200 feet away from Pikes Peak.
Here is a visual representation of what I mean:

Now, the important thing is to find Sentinel Point, but lets look at something real quick.
GPS Coordinates for Pikes Peak: 38.8405322, -105.0442048
GPS Coordinates for Sentinel Point: 38.840500, -105.104700
Using the Distance calculator found
here, we can determine that the distance between Pike's Peak and Sentinel Point is 3.26 miles or 17,212 feet. This is a really good distance to use because Nick is almost directly north of Pikes Peak and these two points are almost directly east/west from each other. That means that Nick should see these points at a fairly close representation to 17,200 feet if he has a good scale of distance to use. Since Nick suggests the visible height of Pikes Peak is 8,000 feet, we can use that to see if this estimate matches reality. using my last screenshot above, we run into a problem. The first sharp peak to the right of Pikes Peak is estimated at about 19,000 feet of ground distance away. That would mean Sentinel Point should be between Pikes Peak and the first sharp peak that we see. This brings us back to the screenshot I got from Peak Finder.
I enlarged (and cropped) the mountains showing in the screenshot until I got Pikes Peak at about the same size and slope we see in Nick's video. This is where things get interesting to me.
Once I placed this enlarged image below the still from the video where the peaks line up, we can see where Sentinel Peak should be. I continued my 8,000 ft segments out to see about how many of these line segments get me from Pikes Peak to Sentinel Point.

When you count the line segments, there is 9 of them. If each line segment roughly represents 8,000 feet, then the distance between Pikes Peak and Sentinel Point is about 72,000 feet away (13.63 miles). We know that's not the case. It would be rather impossible for the visible height to be 8,000 feet in the top picture since it would put Sentinel Point many miles away when it should be only a little more than 3 miles.
Now, with the above image, I decided to look at it a different way. If we presume that the line segment matches the visible height of Pikes Peak, then we can say that Sentinel Point is roughly 9 "visible heights" away from Pikes Peak. we know that the actual distance between the two is 17,212 feet. If we divide that by 9, we get 1,912.4 feet. This would imply, if my estimates are fairly (albeit crudely) accurate, then I would estimate that the visible height of Pikes Peak from the 10:43 in the video is actually around 2,000 feet. With the Standard Refraction calculation on this website, and assuming a base elevation of 9114 feet, I get 6614 feet. Subtract that from 9,114 feet, and I get 2,500 feet. If you consider the variable errors in my crude estimates, the compression an image has because of refraction over long distances, and the possibility that the obstruction at the base of the mountain is higher than the elevation of the viewer, I think my estimate is a fairly accurate one using a screenshot of the video and a screenshot of Peak Finder from the same location.


