ConfusedHominid
New Member
Hello all,
Youtube user Taboo Conspiracy posted two videos in the past few months in which he made the following claim: Curve calculators, featuring Metabunk in particular, do not calculate for the angular size of objects. When ''corrected'' for angular size, such objects would be hidden below the horizon.
- source (description)
Specific Claim and "Method" employed:
The claim made by Taboo Conspiracy is purely a mathematical one.
Video that will be referenced: second video (all time stamps refers to frames).
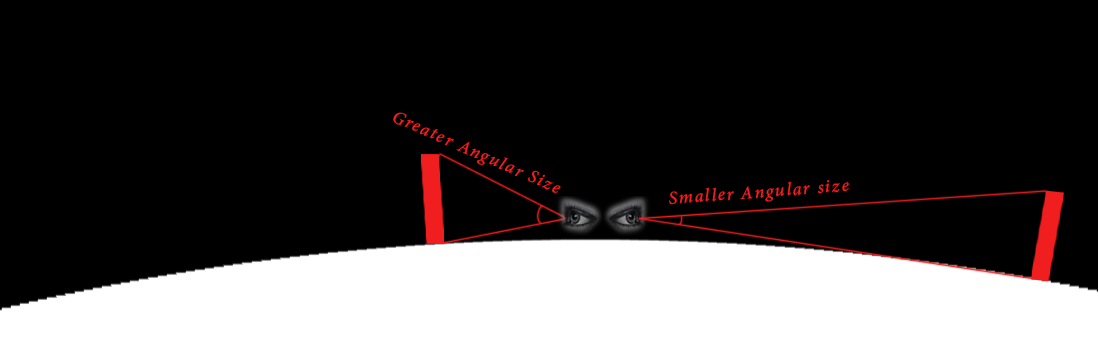
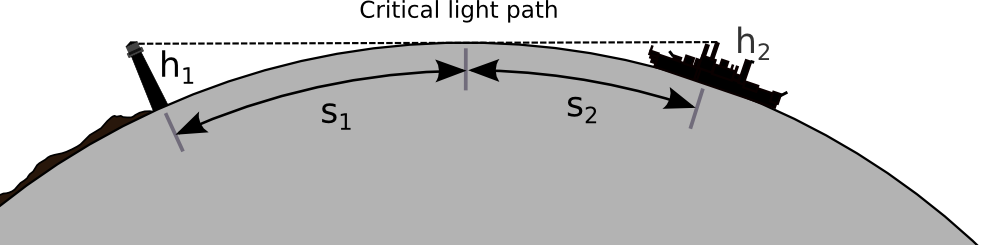
The following two frames (timestamps in the snapshots) sum up the general reason behind his claim:
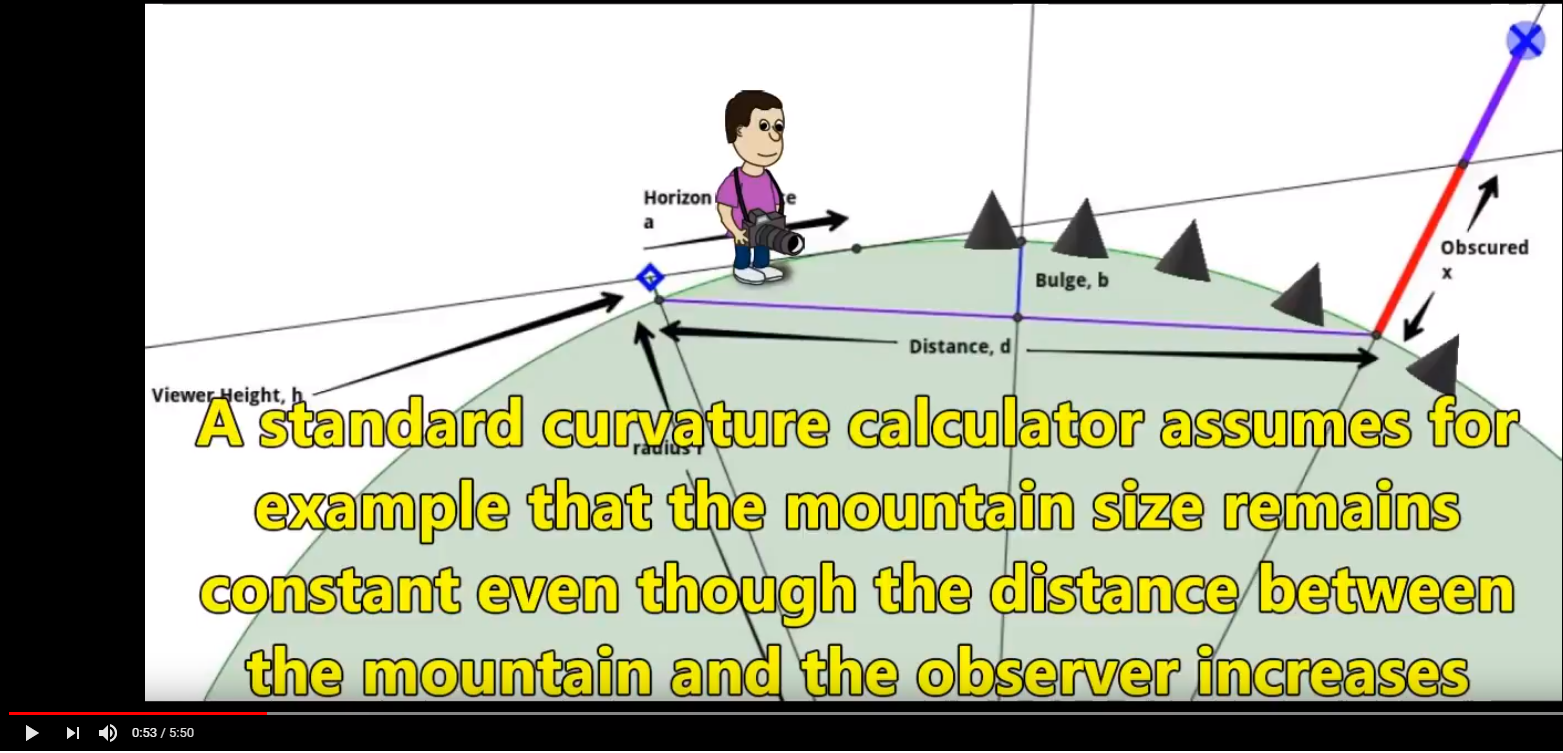
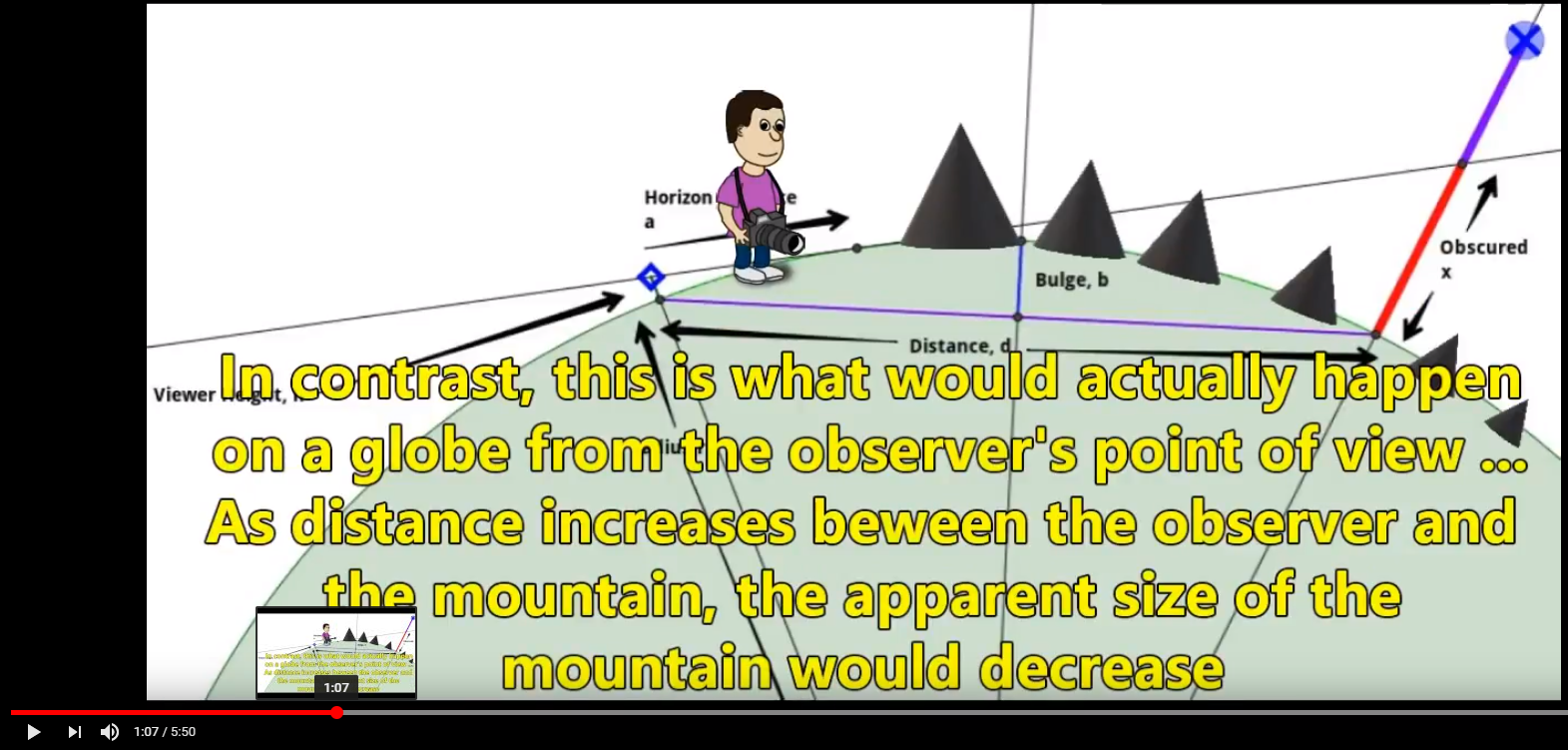
To continue:
[1] At 2:45 (timestamp) he shows off a photo of mt Denali.
Distance from observer: 135 miles, Mountain elevation: 20310 feet, Observer height: 6 feet
As you'll see the entire photo is irrelevant. It'll be purely mathematical.
[2] At 3:05 (timestamp) http://www.ringbell.co.uk/info/hdist.htm is used to calculate the distance to the horizon for a 6 feet observer. The result being 3 miles (15840 feet). No objections here.
[3] At 3:23 (timestamp) he uses http://www.1728.org/angsize.htm to calculate the angular size of Mt Denali (20310 feet) at 3 miles (15840 feet) as if it were at the horizon.
At 15840 feet, Denali (20310 feet elevation) has an angular size of 65.3 degrees.
[4] At 3:45 & 3:55 (timestamp) The next thing Taboo Conspiracy does is increase the distance of Mt Denali to 50 miles (264000 feet) (making the photo irrelevant) and calculate the angular size for Mt Denali at 50 miles.
At 264000 feet, Denali (20310 feet elevation) has an angular size of 4.4 degrees.
[5] At 4:10 (timestamp) Taboo Conspiracy makes a leap I am unable to understand: He divides 4.4 degrees by 65.3 degrees and multiplies the answer by the elevation of mt Denali (20310 feet).
4.4 / 65.3 x 20310 (anyone any idea why he did this?) = 1368.5, or 1369.
According to Taboo Conspiracy this number (1369) is the Apparent Size of Mt Denali in feet at a distance of 50 miles.
[6] At 4:41 He then turns to Metabunk calc, using 50 miles (distance) and 6 feet (observer height), he uses the resulting ["Hidden"] value of 1473 feet.
https://www.metabunk.org/curve/?d=50&h=6&r=3959&u=i&a=n&fd=60&fp=3264
[7] At 5:00 he compares the two values 1369 feet and 1473 feet. The difference being 104 feet, Taboo Conspiracy concludes Mt Denali should be hidden for an observer at a distance of 50 miles. The reason why he thinks we see objects appear above the horizon is because of atmospheric magnification.
My Attempt at Debunking this Claim:
- First off, metabunk's calculations seem to be quite accurate at predicting how much ought to be seen at various distances. If one were to take Taboo's assertions and math at face value, they are already suspect.
- The assertion that metabunk doesn't account for differences in angular size is unsupported.
- When Taboo gets to [5], I see math that doesn't seem right to me. I don't see the logic in converting an angular size in degrees to apparent size in feet. Mostly because an object has an absolute size in feet and an apparent angular size.
The way I reason: for an object to appear 1369 feet in "apparent" size at 50 miles, the object has to be literally 1369 feet. The only way I can somehow grasp Taboo's argument is by changing the statement to: Mt Denali viewed from 50 miles (6 foot tall observer) should have an angular size smaller than the angular size of the horizon at 3 miles.
Need Help in Debunking:
I am quite bad at math and thus am not able to provide a better picture on:
- Does Metabunk Calculator take into account for Angular Size? If yes, how?
- Is it valid to convert angular degrees to apparent size in feet? Is Taboo's math for this valid? How precisely is it invalid?
Anyone willing to help out this hominid?
Youtube user Taboo Conspiracy posted two videos in the past few months in which he made the following claim: Curve calculators, featuring Metabunk in particular, do not calculate for the angular size of objects. When ''corrected'' for angular size, such objects would be hidden below the horizon.
- source (description)
Specific Claim and "Method" employed:
The claim made by Taboo Conspiracy is purely a mathematical one.
Video that will be referenced: second video (all time stamps refers to frames).
The following two frames (timestamps in the snapshots) sum up the general reason behind his claim:


To continue:
[1] At 2:45 (timestamp) he shows off a photo of mt Denali.
Distance from observer: 135 miles, Mountain elevation: 20310 feet, Observer height: 6 feet
As you'll see the entire photo is irrelevant. It'll be purely mathematical.
[2] At 3:05 (timestamp) http://www.ringbell.co.uk/info/hdist.htm is used to calculate the distance to the horizon for a 6 feet observer. The result being 3 miles (15840 feet). No objections here.
[3] At 3:23 (timestamp) he uses http://www.1728.org/angsize.htm to calculate the angular size of Mt Denali (20310 feet) at 3 miles (15840 feet) as if it were at the horizon.
At 15840 feet, Denali (20310 feet elevation) has an angular size of 65.3 degrees.
[4] At 3:45 & 3:55 (timestamp) The next thing Taboo Conspiracy does is increase the distance of Mt Denali to 50 miles (264000 feet) (making the photo irrelevant) and calculate the angular size for Mt Denali at 50 miles.
At 264000 feet, Denali (20310 feet elevation) has an angular size of 4.4 degrees.
[5] At 4:10 (timestamp) Taboo Conspiracy makes a leap I am unable to understand: He divides 4.4 degrees by 65.3 degrees and multiplies the answer by the elevation of mt Denali (20310 feet).
4.4 / 65.3 x 20310 (anyone any idea why he did this?) = 1368.5, or 1369.
According to Taboo Conspiracy this number (1369) is the Apparent Size of Mt Denali in feet at a distance of 50 miles.
[6] At 4:41 He then turns to Metabunk calc, using 50 miles (distance) and 6 feet (observer height), he uses the resulting ["Hidden"] value of 1473 feet.
https://www.metabunk.org/curve/?d=50&h=6&r=3959&u=i&a=n&fd=60&fp=3264
[7] At 5:00 he compares the two values 1369 feet and 1473 feet. The difference being 104 feet, Taboo Conspiracy concludes Mt Denali should be hidden for an observer at a distance of 50 miles. The reason why he thinks we see objects appear above the horizon is because of atmospheric magnification.
My Attempt at Debunking this Claim:
- First off, metabunk's calculations seem to be quite accurate at predicting how much ought to be seen at various distances. If one were to take Taboo's assertions and math at face value, they are already suspect.
- The assertion that metabunk doesn't account for differences in angular size is unsupported.
- When Taboo gets to [5], I see math that doesn't seem right to me. I don't see the logic in converting an angular size in degrees to apparent size in feet. Mostly because an object has an absolute size in feet and an apparent angular size.
The way I reason: for an object to appear 1369 feet in "apparent" size at 50 miles, the object has to be literally 1369 feet. The only way I can somehow grasp Taboo's argument is by changing the statement to: Mt Denali viewed from 50 miles (6 foot tall observer) should have an angular size smaller than the angular size of the horizon at 3 miles.
Need Help in Debunking:
I am quite bad at math and thus am not able to provide a better picture on:
- Does Metabunk Calculator take into account for Angular Size? If yes, how?
- Is it valid to convert angular degrees to apparent size in feet? Is Taboo's math for this valid? How precisely is it invalid?
Anyone willing to help out this hominid?