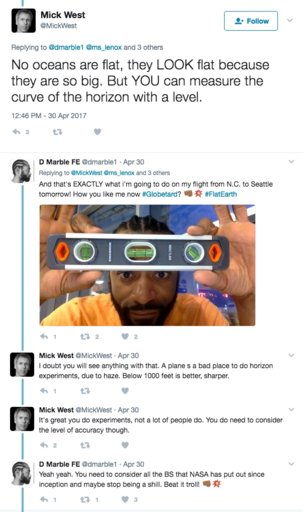
Yes, I meant for staying in the same place horizontally and gaining altitude.Assuming you were standing in the middle of the disk. Which you always (kind of) are on a sphere (the "disk" being in the plane formed by the horizon)
But that's also a good point - on the flat Earth, the horizon would be closer to you in one direction, depending where you were in relation to the edge.