Rory
Closed Account
Perspective is difficult, both to understand and to explain. This was recently brought home to me listening to flat earthers Nathan Oakley and Anthony Riley attempt to explain this photo of mountains in Washington and Oregon:

All decent analyses show that it aligns perfectly well with a globe earth model and is completely incompatible with being on a flat plane, yet the gentlemen in question demonstrated that they are unaware of how viewing angles are calculated, and how perspective works.
The question, then, is how do we explain how perspective works mathematically; show that calculators do include perspective; and help people who don't understand what perspective is, who struggle with maths, and who are mistakenly convinced that they already have the answers?
Theory
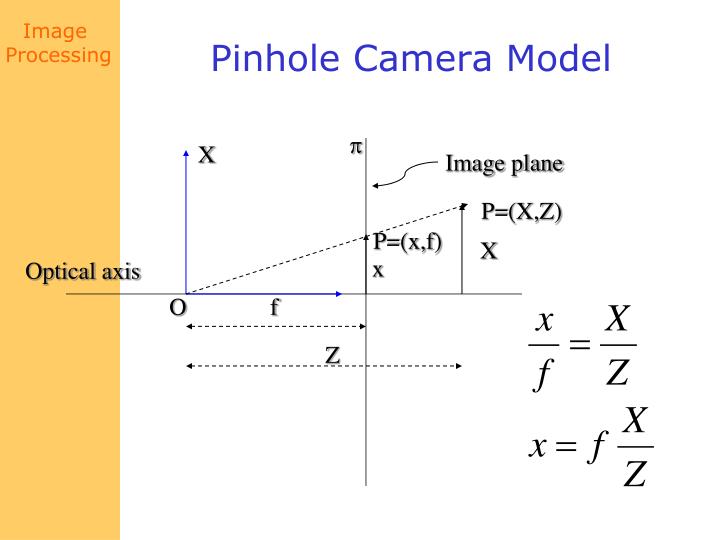
The theory and methodology is fairly straightforward: viewing angles (angle of elevation) between two points can be calculated using trigonometry. These angles will show where something will appear in a photograph, or in our actual field of vision. Larger angles will appear higher and smaller angles will appear lower. To calculate the angle, all we require is distance and elevation.
Here is a picture demonstrating this (angles, distances, and elevations are not to scale):
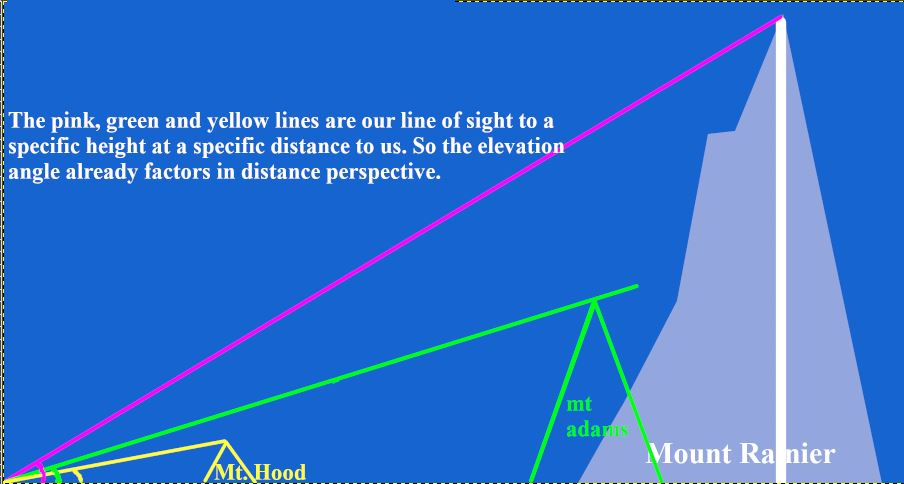
This shows how the line of sight from the observer in the bottom left corner to each of the peaks forms the hypotenuse of a right-angled triangle, which can then be calculated by tan(x)=opposite/adjacent (that is, elevation over distance).
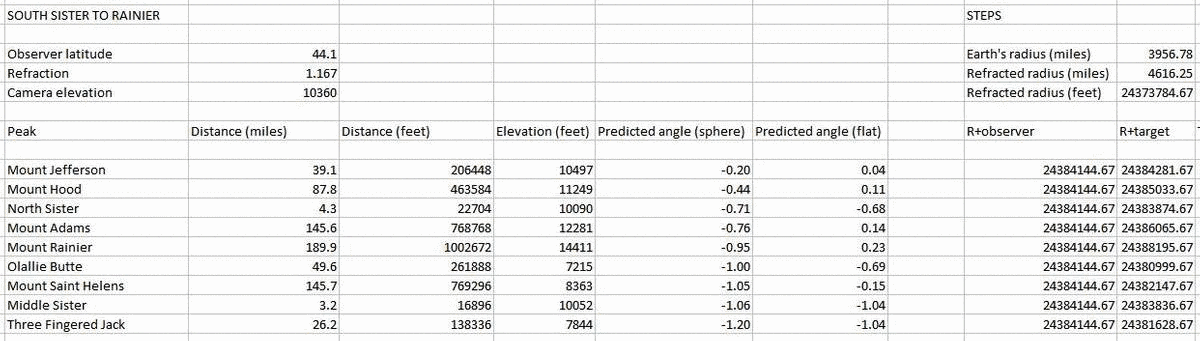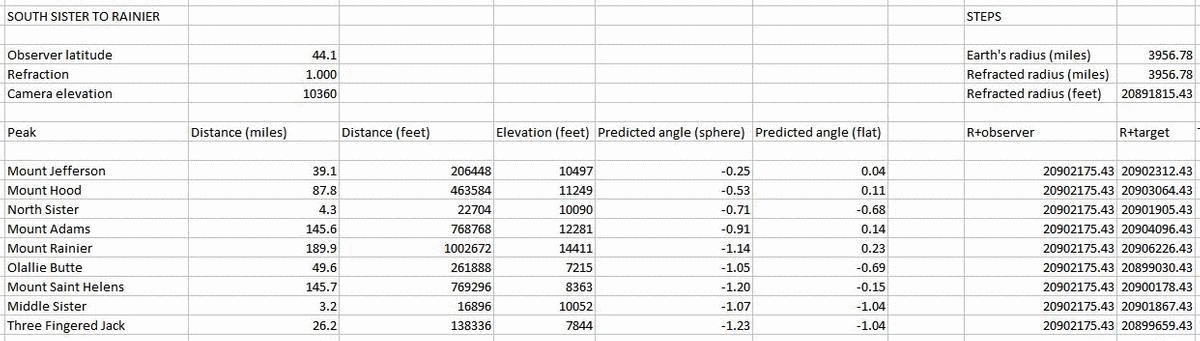
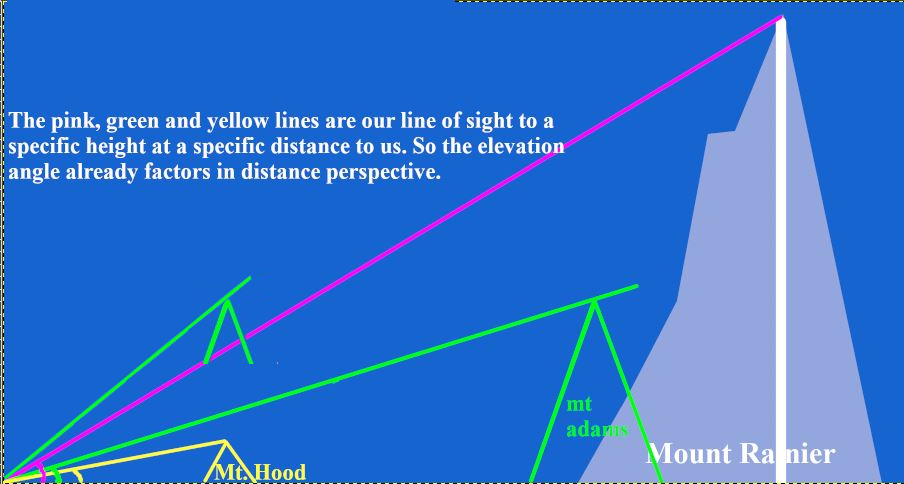
The angle to Mt Rainier is not the largest because it's the tallest mountain, but because of a combination of distance and elevation: if we bring Mt Adams closer to the observer, for example, to the position where Mt Hood is, the angle to its peak will be larger than the angle to Rainier, and it will be predicted to appear highest in a photograph (assuming a flat plane):
Verifying the theory using distant mountains, however, is difficult to do. So we need a way to do this that is available to anyone.
Example
To demonstrate that calculators include perspective, all we need are a list of distances and elevations of some known landmarks and a photograph of these landmarks. Any photograph of a flat-ish street will do, but it would be best if it included buildings of different heights, with some taller buildings in the background.
This one of 5th Avenue in New York, taken at the intersection of E/W17th Street, should be a good candidate (building numbers added):

Here are some of the landmarks seen in this picture:
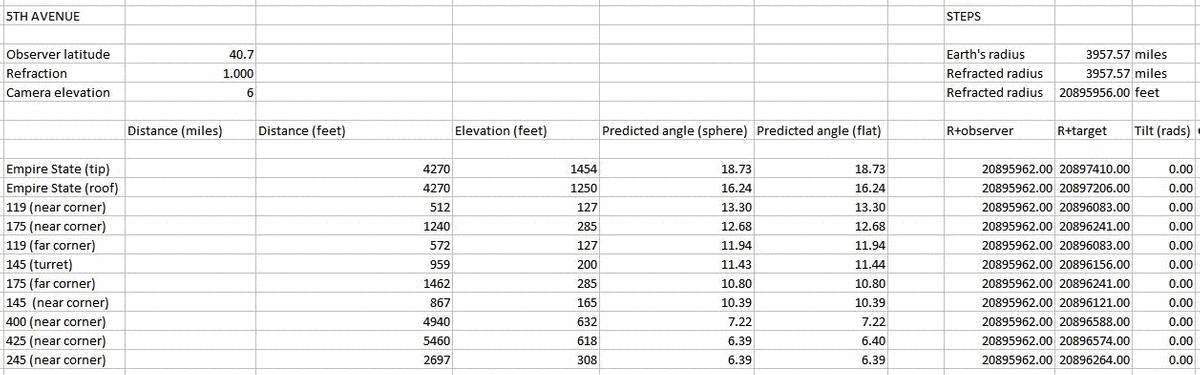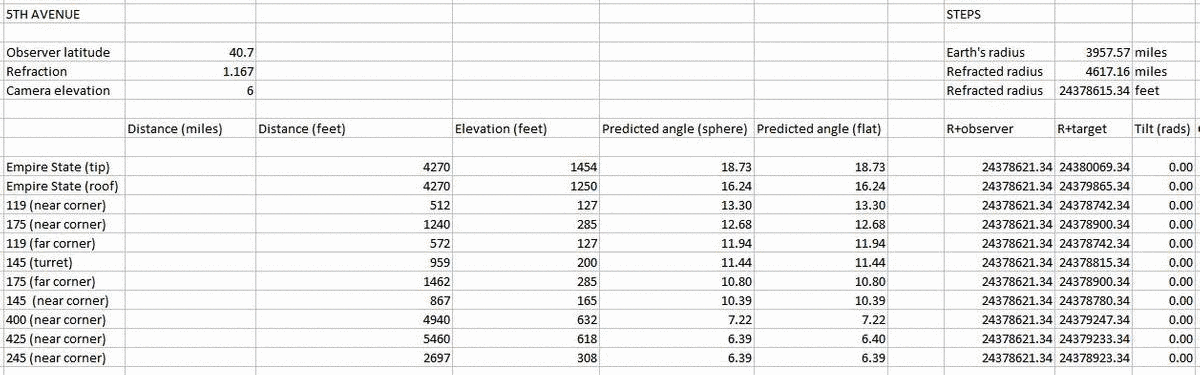
Empire State Building - distance, 4270 feet; height, 1454 feet to tip, 1250 feet to roof
HSBC, 145 5th Avenue - distance, 867 feet to nearest corner, 959 feet to turret; height, 165 feet (roof), 200 feet (turret)
119 5th Avenue - 250 feet to near corner, 455 to far corner; estimated height 130 feet
Flatiron Building, 175 5th Avenue - d. 1240, 1462; h. 285 feet
245 5th Avenue - d. 2697; h. 308 feet
Langham Place, 400 5th Avenue - d. 4940; h. 632 feet
425 5th Avenue - d. 5460; h. 618 feet
Camera height I believe to be very close to 6 feet - certainly within a foot or so - based on the parallel lines in the images, the vehicles, and the people's heads.
Now let's put those figures into a calculator and find the predicted viewing angles by using tan(x)=elevation/distance. The largest angle indicates which building will appear highest in the photo, and so on:
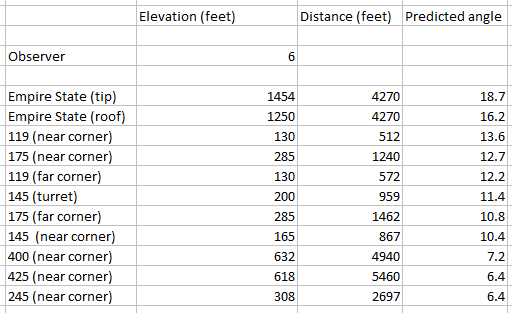
Looking at the photo, we see that the predicted apparent height order and the actual apparent height order are the same:

All decent analyses show that it aligns perfectly well with a globe earth model and is completely incompatible with being on a flat plane, yet the gentlemen in question demonstrated that they are unaware of how viewing angles are calculated, and how perspective works.
The question, then, is how do we explain how perspective works mathematically; show that calculators do include perspective; and help people who don't understand what perspective is, who struggle with maths, and who are mistakenly convinced that they already have the answers?
Theory
The theory and methodology is fairly straightforward: viewing angles (angle of elevation) between two points can be calculated using trigonometry. These angles will show where something will appear in a photograph, or in our actual field of vision. Larger angles will appear higher and smaller angles will appear lower. To calculate the angle, all we require is distance and elevation.
Here is a picture demonstrating this (angles, distances, and elevations are not to scale):
This shows how the line of sight from the observer in the bottom left corner to each of the peaks forms the hypotenuse of a right-angled triangle, which can then be calculated by tan(x)=opposite/adjacent (that is, elevation over distance).
The angle to Mt Rainier is not the largest because it's the tallest mountain, but because of a combination of distance and elevation: if we bring Mt Adams closer to the observer, for example, to the position where Mt Hood is, the angle to its peak will be larger than the angle to Rainier, and it will be predicted to appear highest in a photograph (assuming a flat plane):
Verifying the theory using distant mountains, however, is difficult to do. So we need a way to do this that is available to anyone.
Example
To demonstrate that calculators include perspective, all we need are a list of distances and elevations of some known landmarks and a photograph of these landmarks. Any photograph of a flat-ish street will do, but it would be best if it included buildings of different heights, with some taller buildings in the background.
This one of 5th Avenue in New York, taken at the intersection of E/W17th Street, should be a good candidate (building numbers added):
Here are some of the landmarks seen in this picture:
Empire State Building - distance, 4270 feet; height, 1454 feet to tip, 1250 feet to roof
HSBC, 145 5th Avenue - distance, 867 feet to nearest corner, 959 feet to turret; height, 165 feet (roof), 200 feet (turret)
119 5th Avenue - 250 feet to near corner, 455 to far corner; estimated height 130 feet
Flatiron Building, 175 5th Avenue - d. 1240, 1462; h. 285 feet
245 5th Avenue - d. 2697; h. 308 feet
Langham Place, 400 5th Avenue - d. 4940; h. 632 feet
425 5th Avenue - d. 5460; h. 618 feet
Camera height I believe to be very close to 6 feet - certainly within a foot or so - based on the parallel lines in the images, the vehicles, and the people's heads.
Now let's put those figures into a calculator and find the predicted viewing angles by using tan(x)=elevation/distance. The largest angle indicates which building will appear highest in the photo, and so on:
Looking at the photo, we see that the predicted apparent height order and the actual apparent height order are the same:
Last edited: