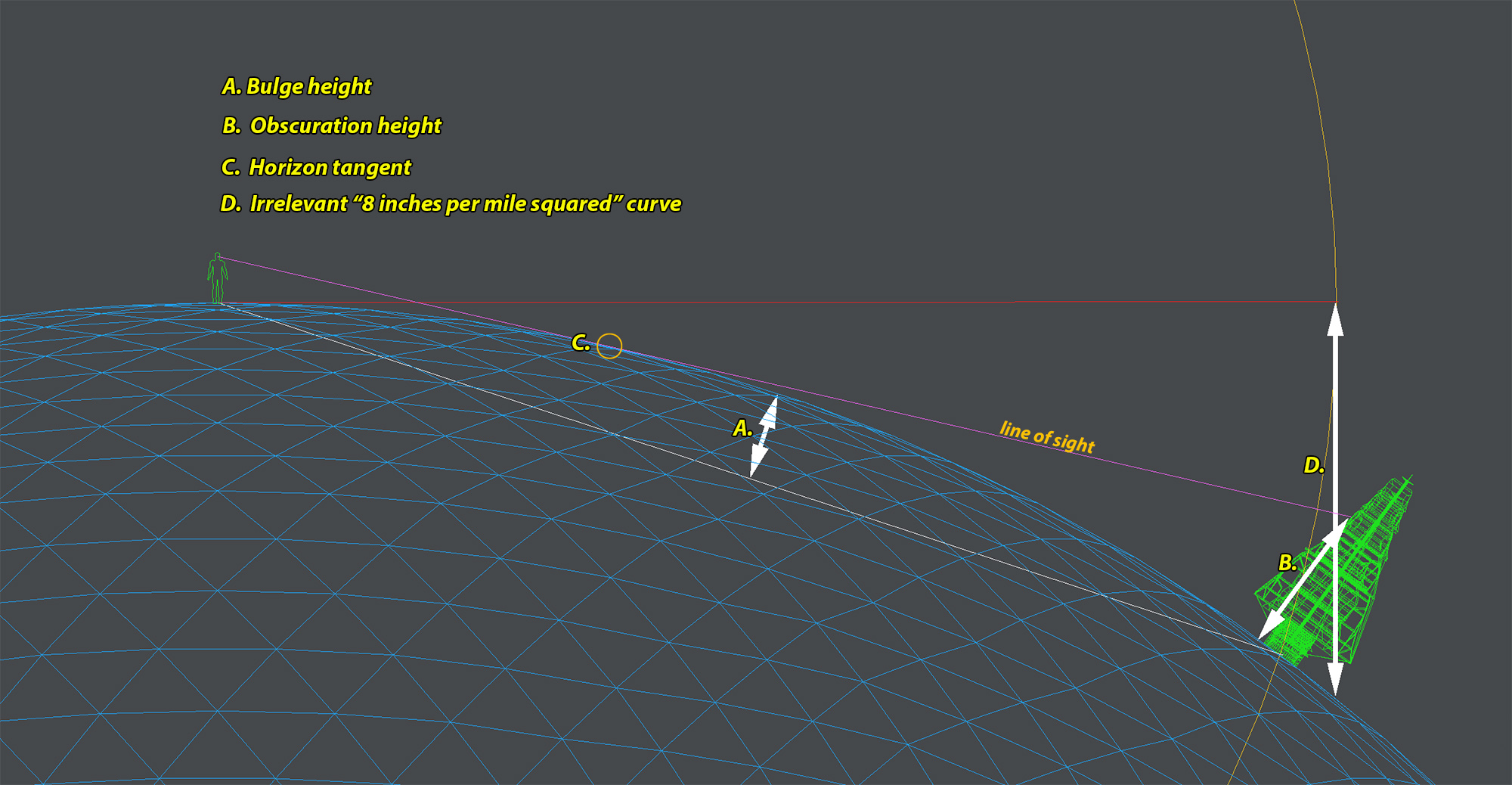
When people talk about 'curvature' they're generally talking about the curve between you (the observer) and the horizon, or something beyond the horizon. The curve, of course, cannot be detected with the naked eye, but its effects can, such as the obscuration of the lower parts of distant buildings and ships.
The 'left to right' curve is something different, and cannot be seen until you're way up there. At least 60,000 feet, and more like 100,000 feet for it to be significantly pronounced.
To demonstrate:
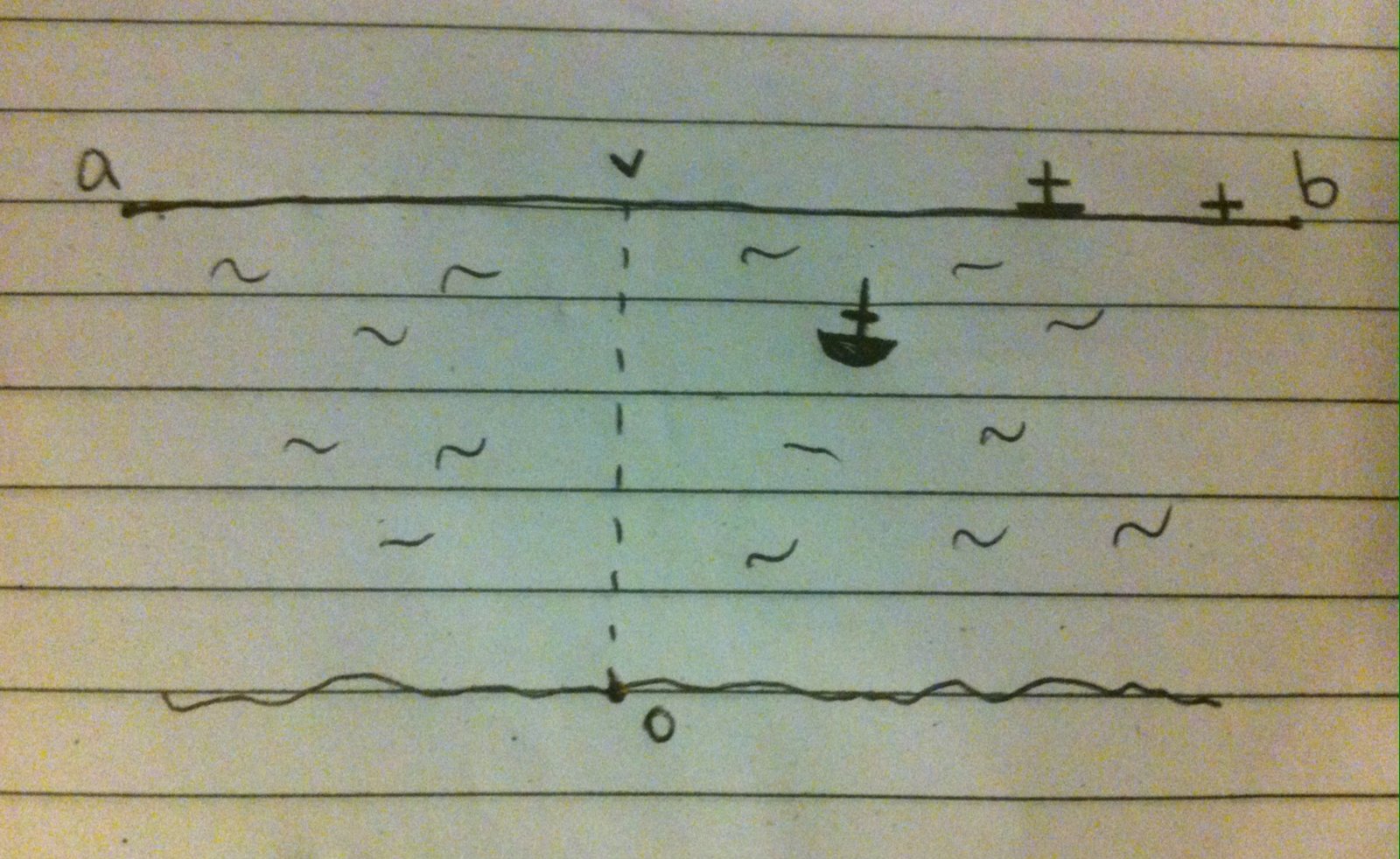
The line ab is the horizon. The observer is at o. The object you're looking at is at v.
When people talk about curvature, and use the curvature calculator, it's the line ov that they're measuring: the "straight ahead" curve.
Determining the curvature for the horizon - for ab - is an altogether different calculation, as outlined above.
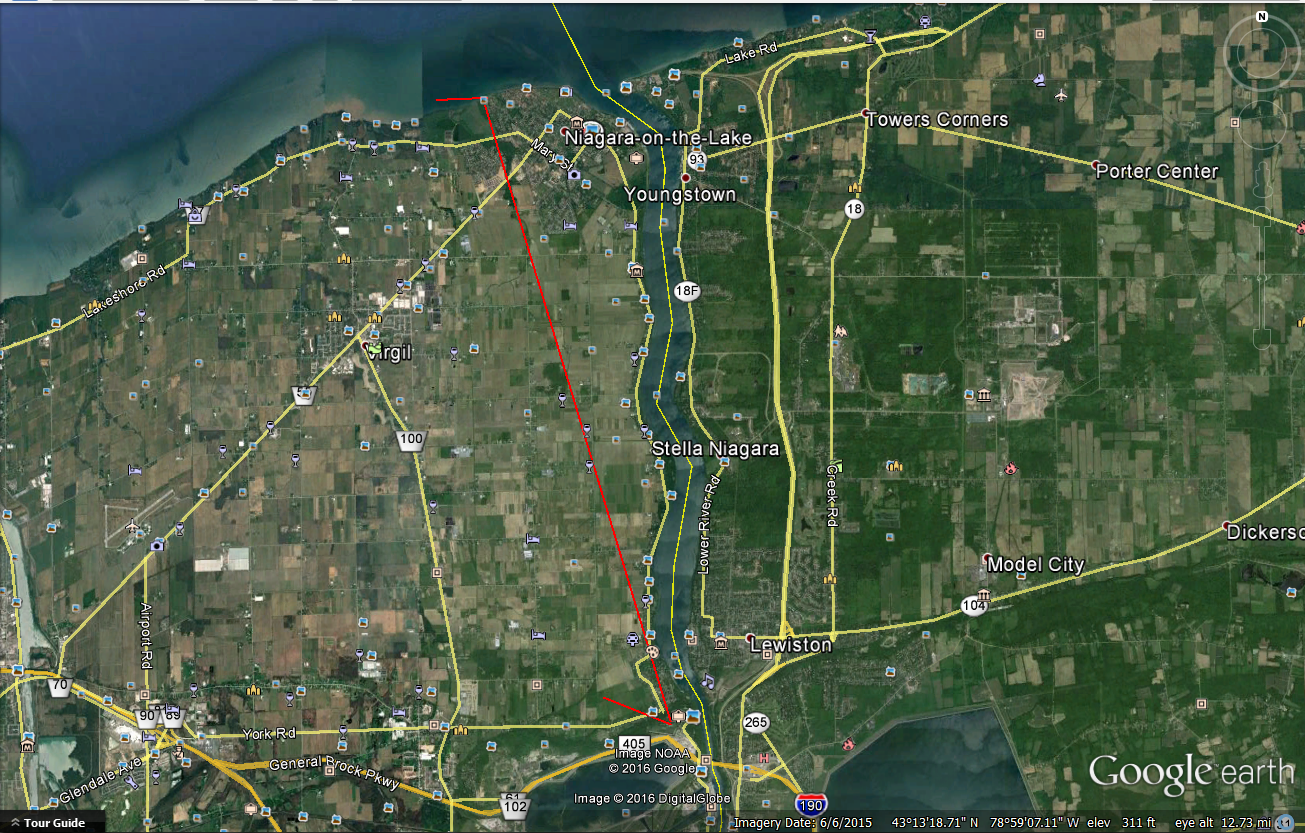
For "viewer height in feet" just put in the difference between the viewer and the lake (ie, the elevation of the horizon).
Yep, that's right. Will be interesting to see how much of the SkyDome you can see, and how it compares to this photo: