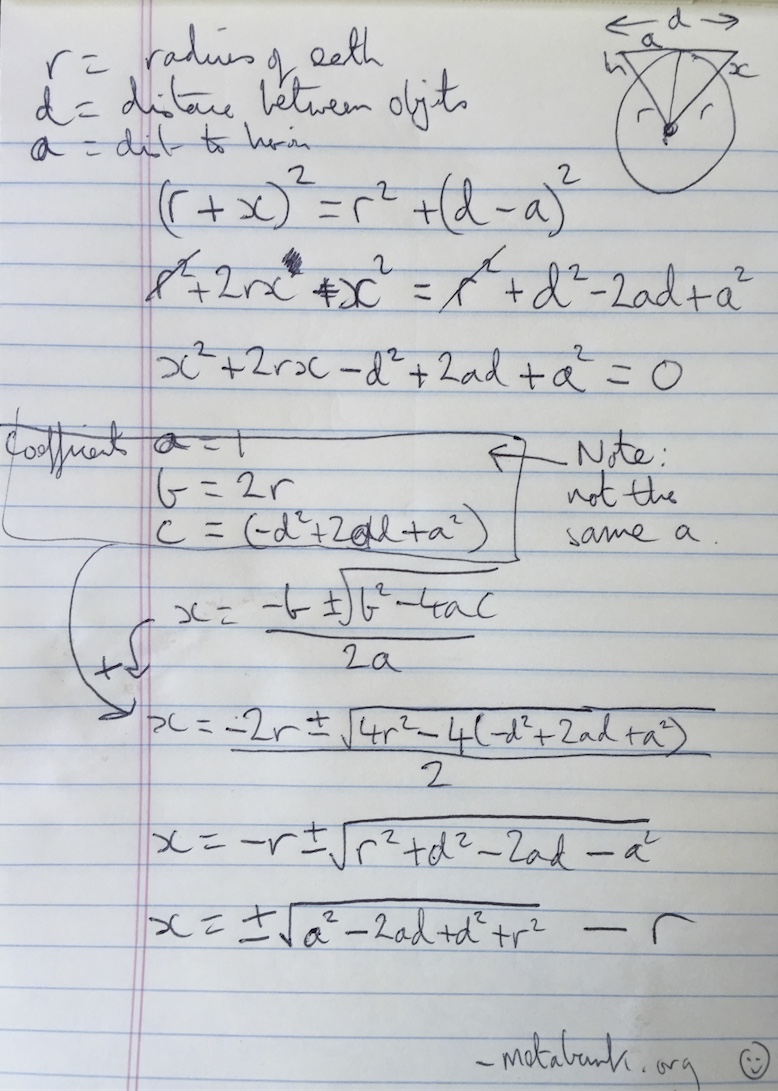https://www.metabunk.org/curve/
To use it you just put in the distance to the object in miles and your height above the surface in feet.
The Metabunk curve calculator was written to provide a simple answer to the question: "how much of a distant object is hidden by the curve of the earth from a certain distance and view position". The following diagram is an exaggerated look at the numbers involved.
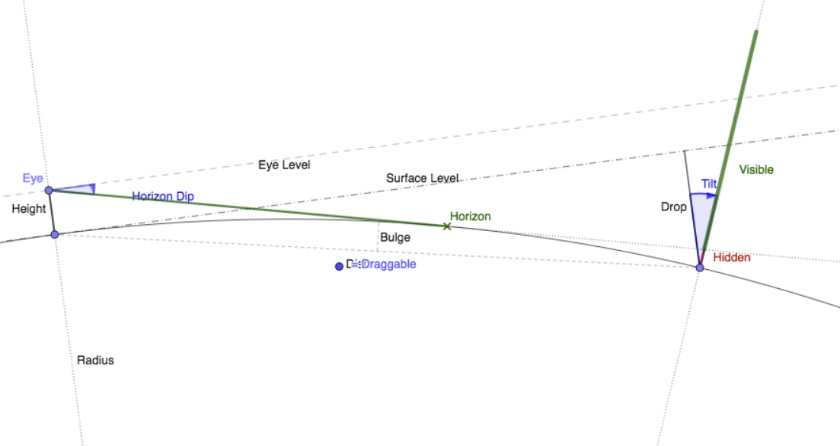
There's a version of this diagram on the calculator page that you can move around.
Notice there are two sets of results given, "Results ignoring refraction" and "With Standard Refraction".
The results ignoring refraction are the results if we ignore the effects of the air (the atmosphere) between the viewer (the eye position) and the target object.
When light passes though air that varies in density then it gets bent towards the higher density air. Normally air gets less dense as you go higher (think of thin air at the top of a mountain). When the light is bent down then it makes things look higher than they are. It can also bend the light around the curve of the earth.
This has the effect of (visually) flattening the Earth a bit, and we can use a hand rule of thumb (used by surveyors for 100+ years) of just doing the same calculation with a larger (7/6x) radius earth. That give you the second set of numbers.
In reality the "ignoring refraction" numbers are almost always going to be too small. The atmosphere always exists, and it's always refracting. On average it's going to give you the "standard refraction" values. However there's going to be considerable variations. "Standard" here refers to the international standard atmosphere which is simply an average state of the atmosphere used as a baseline. It's like there's a "standard" temperature of 66°F/19°C. Again that's an average, over the whole year. On some days it's only going to be 66°F for a few minutes, some days (and/or locations) it's never going to be that value.
So the "standard refraction" is just a typical value. Actual observations will vary.
Once you've got the results, you can save them by clicking on "Permalink
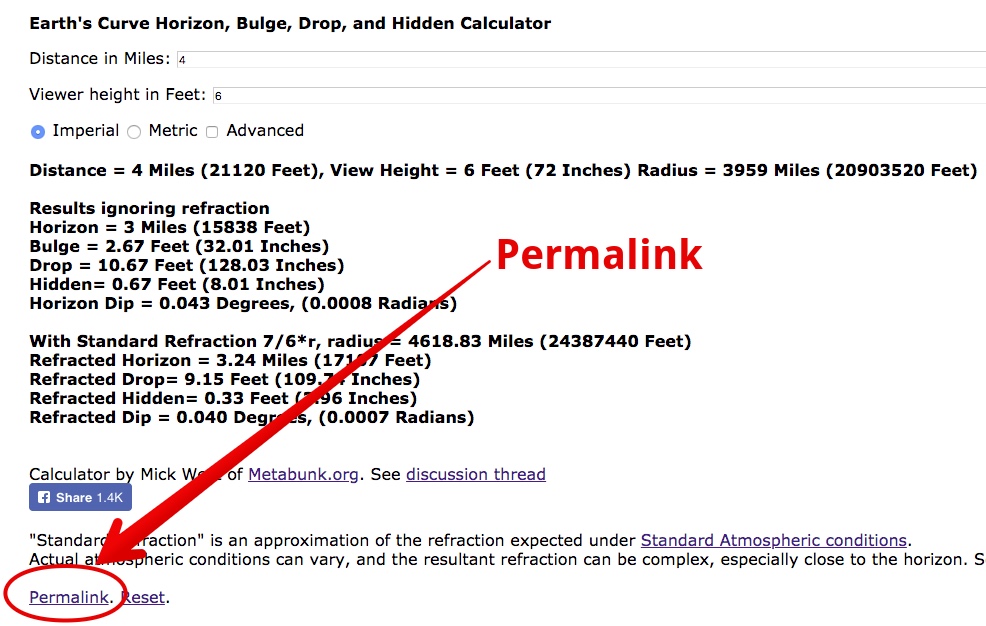
then copy the URL from the browser for sharing. It will look something like:
https://www.metabunk.org/curve/?d=4&h=6&r=3959&u=i&a=n&fd=60&fp=3264
You don't have to click on "permalink" again, the URL will update automatically.
There's also an "Advanced" version (click the "Advanced" checkbox just above the results). This gives you more options, and shows more results and the underlying math.
This calculator arose from discussion in this thread:
https://www.metabunk.org/earth-curv...bunking-flat-concave-earth.t6042/#post-149557
To use it you just put in the distance to the object in miles and your height above the surface in feet.
The Metabunk curve calculator was written to provide a simple answer to the question: "how much of a distant object is hidden by the curve of the earth from a certain distance and view position". The following diagram is an exaggerated look at the numbers involved.
There's a version of this diagram on the calculator page that you can move around.
Notice there are two sets of results given, "Results ignoring refraction" and "With Standard Refraction".
The results ignoring refraction are the results if we ignore the effects of the air (the atmosphere) between the viewer (the eye position) and the target object.
When light passes though air that varies in density then it gets bent towards the higher density air. Normally air gets less dense as you go higher (think of thin air at the top of a mountain). When the light is bent down then it makes things look higher than they are. It can also bend the light around the curve of the earth.
This has the effect of (visually) flattening the Earth a bit, and we can use a hand rule of thumb (used by surveyors for 100+ years) of just doing the same calculation with a larger (7/6x) radius earth. That give you the second set of numbers.
In reality the "ignoring refraction" numbers are almost always going to be too small. The atmosphere always exists, and it's always refracting. On average it's going to give you the "standard refraction" values. However there's going to be considerable variations. "Standard" here refers to the international standard atmosphere which is simply an average state of the atmosphere used as a baseline. It's like there's a "standard" temperature of 66°F/19°C. Again that's an average, over the whole year. On some days it's only going to be 66°F for a few minutes, some days (and/or locations) it's never going to be that value.
So the "standard refraction" is just a typical value. Actual observations will vary.
Once you've got the results, you can save them by clicking on "Permalink
then copy the URL from the browser for sharing. It will look something like:
https://www.metabunk.org/curve/?d=4&h=6&r=3959&u=i&a=n&fd=60&fp=3264
You don't have to click on "permalink" again, the URL will update automatically.
There's also an "Advanced" version (click the "Advanced" checkbox just above the results). This gives you more options, and shows more results and the underlying math.
This calculator arose from discussion in this thread:
https://www.metabunk.org/earth-curv...bunking-flat-concave-earth.t6042/#post-149557
Last edited: