Tony and econ,
I have followed this thread, and I have read the critical pages 242-245 of the Nordenson report, plus a few pages before and after that. Now I haven't read the entire Appendix B, which starts on page 210 in my PDF reader, and not being an engineer, this is a tough read, so I haven't succeeded yet in wrapping my mind fully around Nordenson's approach and argument. Consequently, I can't decide yet whose arguments I accept as correct here.
First, do you agree that Nordenson's approach, model and values (Sections B1-B4) are nearly enough valid to derive a plausible answer to the question whether or not the falling girder would fail the girder connection below in vertical shear?
econ, knowing you, I 'd guess you are in general agreement, or else you wouldn't even start to engage in a discussion of B5.
Tony, you have of course raised objections - let me see if I understand them correctly, at least roughly:
B1: Nordenson summarizes his approach thusly: "
The basis for the analysis was an energy comparison...
(Potential Energy of Falling Floor Slab) + (Energy Dissipated in Failure of Floor) vs. Energy Required to Fail Girder Connection to Column at Floor Below"
<- Tony, I read you as claiming that Nordenson is missing an additional term, namely (Energy Dissipated by falling Floor through Impact with Floor Below). Correct?
Nordensen lists several energy sinks for the term (Energy Dissipated in Failure of Floor) - they include "Plastic deformation of falling girder tip at impact with floor below", but do not include elastic and plastic bending of the falling girder along its entire length at impact.
<- Tony, again, that's what you say is missing and must be included?
And then the deciding step: "
This potential energy at impact was then converted to an equivalent static force based on the stiffness of the impact location and the resulting girder deflection. The resulting shear force transferred to the connection at Column 79 was then calculated and compared with the expected shear capacity of the connection to determine whether the failure of one floor would cause the failure of the floor below."
<- Tony, you argue that the missing term would be correctly inlcuded into the energy comparison by using the stiffness formula for springs in series, right?
B2: Nordenson makes some assumptions about DL, SDL and LL
- reasonable?
He then describes how he modeled the connection failure on fl 13 and shows the geometry of floor deformations that result in SAP2000 -
seems all plausible?
B3: Presents several failure modes that the falling girder and supported beams and slab would experience, and long lists of input values for the dimensions and properties of the floor elements result in some numbers for energy dissipation.
<- Do you accept, at least tentatively, that Nordenson worked with due diligence and introduces no significant error here?
B4: The weight of the falling girder + beams + floors is determined as 46,000 pounds, and the drop height of its center of gravity at the moment of impact as 83 inches (for floor 13) - roughly half a story height, the product is 3818 kip-inches, from which he subtracts 345 kip-inches, the already dissipated energy derived im B4 (detailed numbers in Table B6-1) - so roughly 90% of the PE is available to wreak havoc going into B5
<- Are you ok with these numbers, at least in a ballpark sort of way?
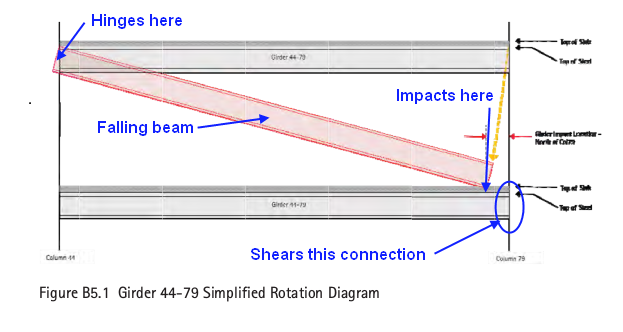
B5.1: I think we will all agree that the end of the falling girder impacts the girder below impacts a few inches away from the column - 10-12 inches seem plausible?
B5.2: Girder stiffness of the fixed girder below derived correctly?
So those are the premises going into B5.3 - the conversion of kinetic energy to a static force by computing
how far the lower girder deflects when it dissipates all that kinetic energy.
<- And that's where Tony disagrees: He claims that the falling girder would deflect too and dissipate energy, and even more as it is less stiff - and that reduces the equivalent force. <- And I agree with Tony! Unless, of course, I am missing something that I haven't been explained by econ 
Over to you!